ГДЗ Геометрія 7 клас Бевз (2024)

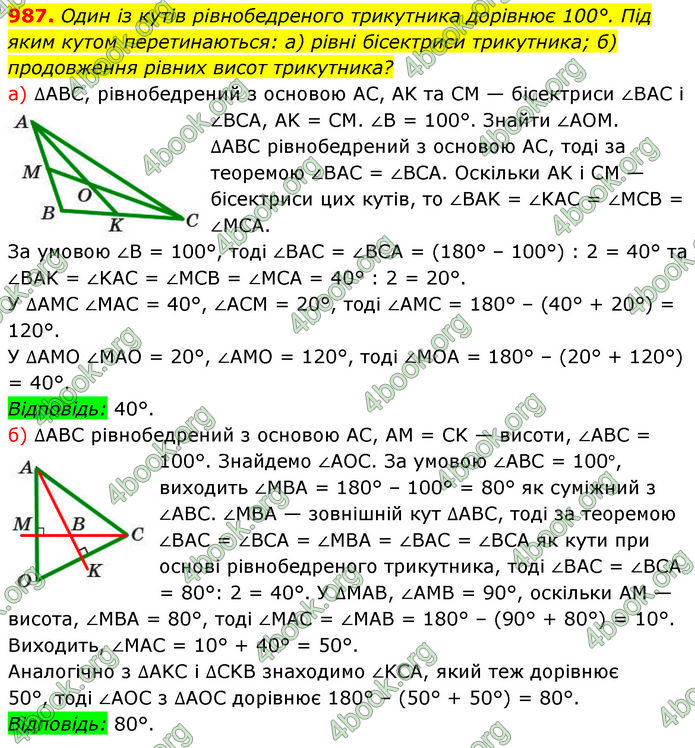
Один із кутів рівнобедреного трикутника дорівнює 100°. Під яким кутом перетинаються: а) рівні бісектриси трикутника; б) продовження рівних висот трикутника? 

а) ∆ABC, рівнобедрений з основою AC, AK та CM — бісектриси ∠BAC і ∠BCA, AK = CM. ∠B = 100°.
Знайти ∠AOM. ∆ABC рівнобедрений з основою AC, тоді за теоремою ∠ВАС = ∠BCA.
Оскільки AK і CM — бісектриси цих кутів, то ∠BAK = ∠KAC = ∠MCB = ∠MCA.
За умовою ∠B = 100°, тоді ∠BAC = ∠BCA = (180° – 100°) : 2 = 40° та ∠BAK = ∠KAC = ∠MCB = ∠MCA = 40° : 2 = 20°.
У ∆AMC ∠MAC = 40°, ∠ACM = 20°, тоді ∠AMC = 180° – (40° + 20°) = 120°.
У ∆AMO ∠MAO = 20°, ∠AМO = 120°, тоді ∠MOA = 180° – (20° + 120°) = 40°.
Відповідь: 40°.
б) ∆ABC рівнобедрений з основою AC, AM = CK — висоти, ∠ABC = 100°.
Знайдемо ∠AOC. За умовою ∠ABC = 100°, виходить ∠MBA = 180° – 100° = 80° як суміжний з ∠ABC.
∠MBA — зовнішній кут ∆ABC, тоді за теоремою ∠ВАС = ∠BCA = ∠MBA = ∠ВАС = ∠BCA як кути при основі рівнобедреного трикутника, тоді ∠ВАС = ∠BCA = 80°: 2 = 40°.
У ∆МАВ, ∠AMB = 90°, оскільки AM — висота, ∠MBA = 80°, тоді ∠МАС = ∠МАВ = 180° – (90° + 80°) = 10°.
Виходить, ∠MAC = 10° + 40° = 50°.
Аналогічно з ∆AKC і ∆CKB знаходимо ∠KCA, який теж дорівнює 50°, тоді ∠AOC з ∆АОС дорівнює 180° – (50° + 50°) = 80°.
Відповідь: 80°.