ГДЗ Геометрія 7 клас Бевз (2024)

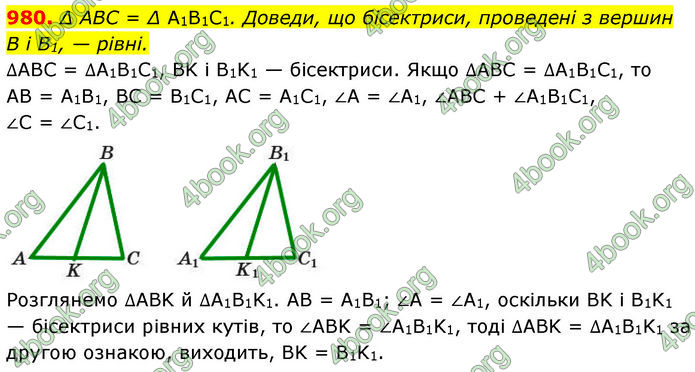
∆ABC = ∆A1B1C1. Доведи, що бісектриси, проведені з вершин B і B1, — рівні. 

∆ABC = ∆A1B1C1, BK і B1K1 — бісектриси.
Якщо ∆ABC = ∆A1B1C1, то AB = A1B1, BC = B1C1, AC = A1C1, ∠A = ∠A1, ∠ABC + ∠A1B1C1, ∠C = ∠C1.
Розглянемо ∆ABK й ∆A1B1K1. AB = A1B1; ∠A = ∠A1, оскільки BK і B1K1 — бісектриси рівних кутів, то ∠ABK = ∠A1B1K1, тоді ∆ABK = ∆A1B1K1 за другою ознакою, виходить, BK = B1K1.