ГДЗ Геометрія 7 клас Бевз (2024)

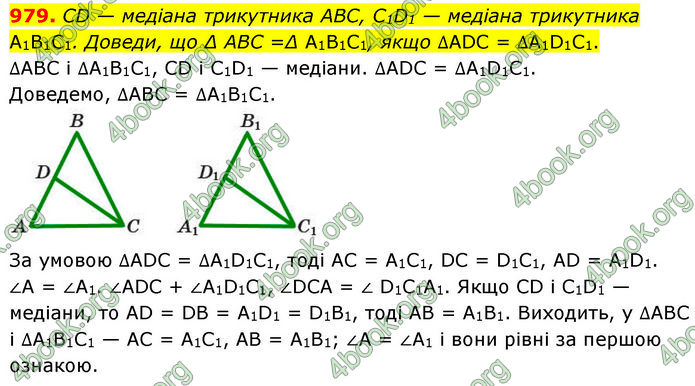
CD — медіана трикутника ABC, C1D1 — медіана трикутника A1B1C1. Доведи, що ∆ ABC =∆ А1В1С1, якщо ∆ADC = ∆A1D1C1. 

∆ABC і ∆А1В1С1, CD і C1D1 — медіани. ∆ADC = ∆A1D1C1.
Доведемо, ∆ABC = ∆A1B1C1. За умовою ∆ADC = ∆A1D1C1, тоді AC = A1C1, DC = D1C1, AD = A1D1.
∠A = ∠A1. ∠ADC + ∠A1D1C1, ∠DCA = ∠ D1C1A1.
Якщо CD і С1D1 — медіани, то AD = DB = A1D1 = D1B1, тоді AB = A1B1.
Виходить, у ∆ABC і ∆A1B1C1 — AC = A1C1, AB = A1B1; ∠A = ∠A1 і вони рівні за першою ознакою.