ГДЗ Геометрія 7 клас Бевз (2024)

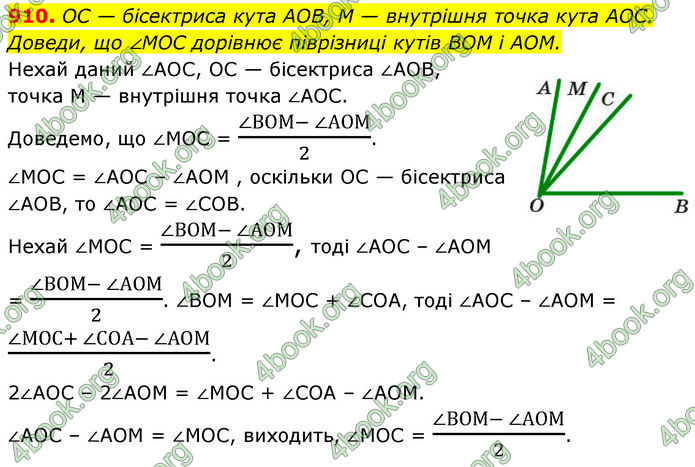
OC — бісектриса кута AOB, M — внутрішня точка кута AOC. Доведи, що ∠MOC дорівнює піврізниці кутів BOM і AOM. 

Нехай даний ∠AOC, OC — бісектриса ∠AOB, точка M — внутрішня точка ∠AOC.
Доведемо, що ∠MOC = (∠ВОМ- ∠АОМ)/2.
∠MOC = ∠AOC – ∠AOM , оскільки OC — бісектриса ∠AOB, то ∠AOC = ∠COB.
Нехай ∠МОС = (∠ВОМ- ∠АОМ)/2, тоді ∠АОС – ∠АОМ = (∠ВОМ- ∠АОМ)/2.
∠ВОМ = ∠МОС + ∠СОА, тоді ∠АОС – ∠АОМ = (∠МОС+ ∠СОА- ∠АОМ)/2.
2∠АОС – 2∠АОМ = ∠МОС + ∠СОА – ∠АОМ. ∠АОС – ∠АОМ = ∠МОС, виходить, ∠МОС = (∠ВОМ- ∠АОМ)/2.