Назад
ГДЗ Геометрія 7 клас Мерзляк (2024)
Реклама:
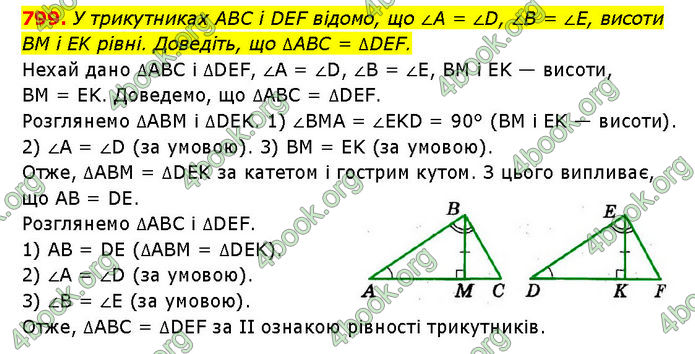
У трикутниках ABC і DEF відомо, що ∠A = ∠D, ∠B = ∠E, висоти BM і EK рівні. Доведіть, що ∆ABC = ∆DEF.
Нехай дано ∆АВС і ∆DEF, ∠A = ∠D, ∠B = ∠E, BM і EK — висоти, BM = EK. Доведемо, що ∆АВС = ∆DEF. Розглянемо ∆ABM і ∆DEK. 1) ∠BMA = ∠EKD = 90° (BM і EK — висоти). 2) ∠A = ∠D (за умовою). 3) BM = EK (за умовою). Отже, ∆ABM = ∆DEK за катетом і гострим кутом. З цього випливає, що AB = DE. Розглянемо ∆ABC і ∆DEF. 1) AB = DE (∆ABM = ∆DEK). 2) ∠A = ∠D (за умовою). 3) ∠B = ∠E (за умовою). Отже, ∆ABC = ∆DEF за II ознакою рівності трикутників.






