ГДЗ Геометрія 7 клас Мерзляк (2024)

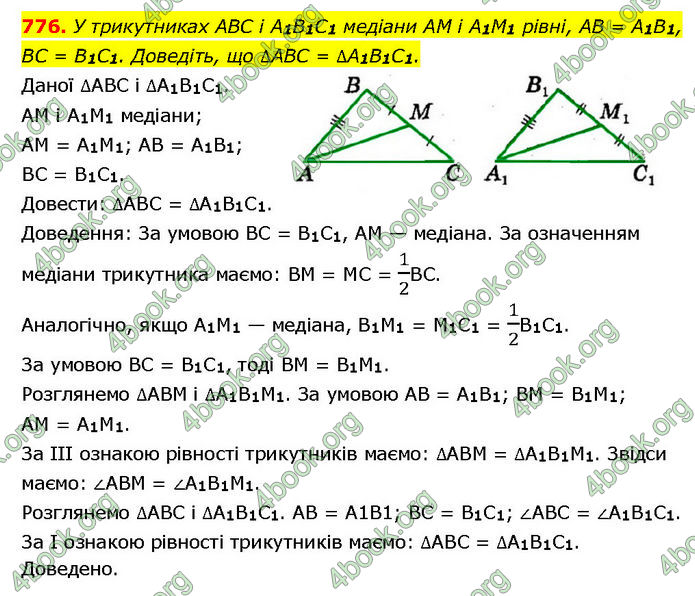
У трикутниках ABC і A1B1C1 медіани AM і A1M1 рівні, AB = A1B1, BC = B1C1. Доведіть, що ∆ABC = ∆A1B1C1.

Даної ∆ABC і ∆A1B1C1. AM і A1M1 медіани; AM = A1M1; AB = A1B1; BC = B1C1. Довести: ∆ABC = ∆A1B1C1. Доведення: За умовою BC = B1C1, AM — медіана. За означенням медіани трикутника маємо: BM = MC = 1/2BC. Аналогічно, якщо A1M1 — медіана, B1M1 = M1C1 = 1/2B1C1. За умовою BC = B1C1, тоді BM = B1M1. Розглянемо ∆ABM і ∆A1B1M1. За умовою AB = A1B1; BM = B1M1; AM = A1M1. За III ознакою рівності трикутників маємо: ∆ABM = ∆A1B1M1. Звідси маємо: ∠ABM = ∠A1B1M1. Розглянемо ∆ABC і ∆A1B1C1. AB = A1B1; BC = B1C1; ∠ABC = ∠A1B1C1. За I ознакою рівності трикутників маємо: ∆ABC = ∆A1B1C1. Доведено.