ГДЗ Геометрія 7 клас Мерзляк (2024)

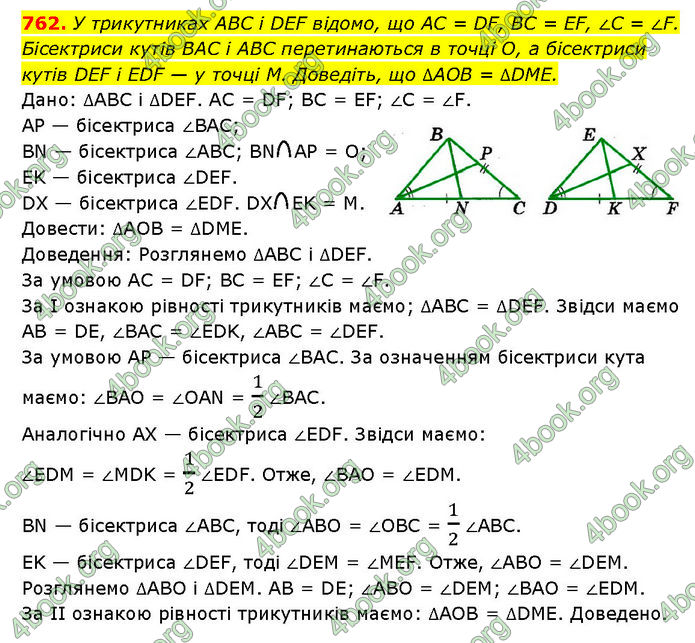
У трикутниках ABC і DEF відомо, що AC = DF, BC = EF, ∠С = ∠F. Бісектриси кутів ВАС і ABC перетинаються в точці О, а бісектриси кутів DEF і EDF — у точці М. Доведіть, що ∆AOB = ∆DME.

Дано: ∆ABC і ∆DEF. AC = DF; BC = EF; ∠C = ∠F. AP — бісектриса ∠BAC; BN — бісектриса ∠ABC; BN AP = O; EK — бісектриса ∠DEF. DX — бісектриса ∠EDF. DX EK = М. Довести: ∆AOB = ∆DME.
Доведення: Розглянемо ∆ABC і ∆DEF. За умовою AC = DF; BC = EF; ∠C = ∠F. За І ознакою рівності трикутників маємо; ∆ABC = ∆DEF. Звідси маємо AB = DE, ∠BAC = ∠EDK, ∠ABC = ∠DEF. За умовою AP — бісектриса ∠BAC. За означенням бісектриси кута маємо: ∠BAO = ∠OAN = 1/2 ∠BAC. Аналогічно AX — бісектриса ∠EDF. Звідси маємо: ∠EDM = ∠MDK = 1/2 ∠EDF. Отже, ∠BAO = ∠EDM. BN — бісектриса ∠ABC, тоді ∠ABO = ∠OBC = 1/2 ∠ABC. EK — бісектриса ∠DEF, тоді ∠DEM = ∠MEF. Отже, ∠ABO = ∠DEM. Розглянемо ∆ABO і ∆DEM. AB = DE; ∠ABO = ∠DEM; ∠BAO = ∠EDM. За II ознакою рівності трикутників маємо: ∆AOB = ∆DME. Доведено.