ГДЗ Геометрія 8 клас Мерзляк (2025)

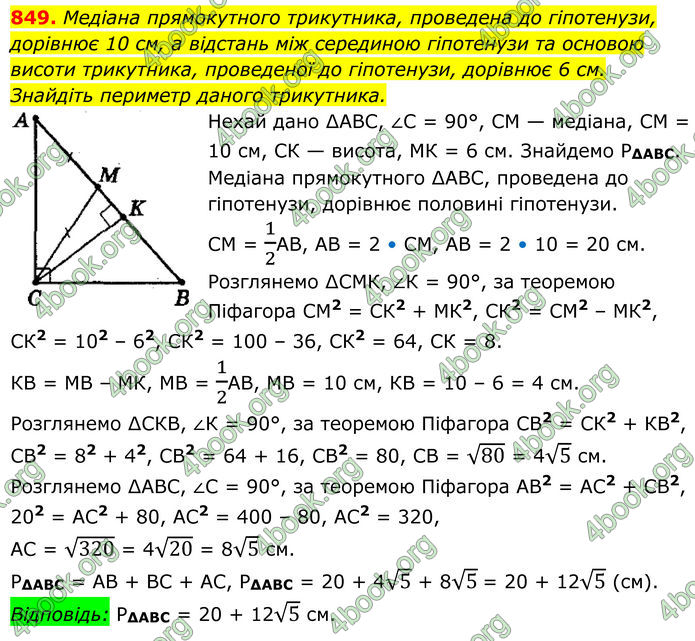
Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 10 см, а відстань між серединою гіпотенузи та основою висоти трикутника, проведеної до гіпотенузи, дорівнює 6 см. Знайдіть периметр даного трикутника.

Нехай дано ∆АВС, ∠С = 90°, СМ — медіана, СМ = 10 см, СК — висота, МК = 6 см.
Знайдемо Р∆ABC. Медіана прямокутного ∆АВС, проведена до гіпотенузи, дорівнює половині гіпотенузи. СМ = 1/2АВ, АВ = 2 • СМ, АВ = 2 • 10 = 20 см.
Розглянемо ∆СМК, ∠К = 90°, за теоремою Піфагора СМ2 = СК2 + МК2, СК2 = СМ2 – МК2, СК2 = 102 – 62, СК2 = 100 – 36, СК2 = 64, СК = 8. КВ = МВ – МК, МВ = 1/2АВ, МВ = 10 см, КВ = 10 – 6 = 4 см.
Розглянемо ∆СКВ, ∠К = 90°, за теоремою Піфагора СВ2 = СК2 + КВ2, СВ2 = 82 + 42, СВ2 = 64 + 16, СВ2 = 80, СВ = √80 = 4√5 см.
Розглянемо ∆АВС, ∠С = 90°, за теоремою Піфагора АВ2 = АС2 + СВ2, 202 = АС2 + 80, АС2 = 400 – 80, АС2 = 320, АС = √320 = 4√20 = 8√5 см.
P∆ABC = AB + BC + AC, P∆ABC = 20 + 4√5 + 8√5 = 20 + 12√5 (см).
Відповідь: P∆ABC = 20 + 12√5 см.