ГДЗ Геометрія 8 клас Мерзляк (2025)

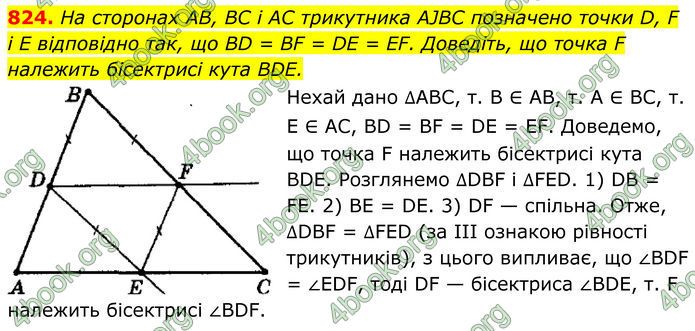
На сторонах AB, BC і AC трикутника AJBC позначено точки D, F i E відповідно так, що BD = BF = DE = EF. Доведіть, що точка F належить бісектрисі кута BDE.

Нехай дано ∆АВС, т. В ∈ АВ, т. А ∈ ВС, т. Е ∈ АС, ВD = ВF = DЕ = ЕF.
Доведемо, що точка F належить бісектрисі кута ВDЕ.
Розглянемо ∆DВF і ∆FЕD. 1) DВ = FЕ. 2) ВЕ = DЕ. 3) DF — спільна.
Отже, ∆DВF = ∆FЕD (за III ознакою рівності трикутників), з цього випливає, що ∠ВDF = ∠ЕDF, тоді DF — бісектриса ∠ВDЕ, т. F належить бісектрисі ∠ВDF.