ГДЗ Геометрія 8 клас Мерзляк (2025)

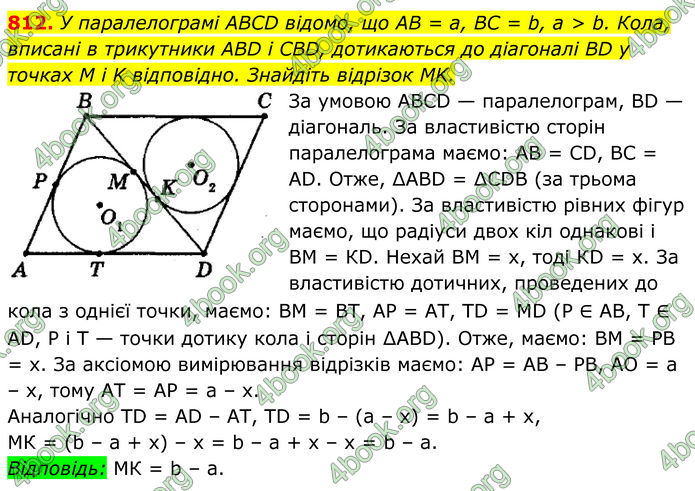
У паралелограмі ABCD відомо, що AB = a, BC = b, а > b. Кола, вписані в трикутники ABD і CBD, дотикаються до діагоналі BD у точках M і K відповідно. Знайдіть відрізок MK.

За умовою АВСD — паралелограм, ВD — діагональ.
За властивістю сторін паралелограма маємо: АВ = СD, ВС = АD. Отже, ∆АВD = ∆СDВ (за трьома сторонами).
За властивістю рівних фігур маємо, що радіуси двох кіл однакові і ВМ = КD. Нехай ВМ = х, тоді КD = х.
За властивістю дотичних, проведених до кола з однієї точки, маємо: ВМ = ВТ, АР = АТ, ТD = MD (Р ∈ АВ, Т ∈ АD, Р і Т — точки дотику кола і сторін ∆АВD). Отже, маємо: ВМ = РВ = х.
За аксіомою вимірювання відрізків маємо: АР = АВ – РВ, АО = а – х, тому АТ = АР = а – х.
Аналогічно ТD = АD – АТ, ТD = b – (а – х) = b – а + х, МК = (b – а + х) – х = b – а + x – x = b – а.
Відповідь: МК = b – а.