ГДЗ Геометрія 8 клас Мерзляк (2025)

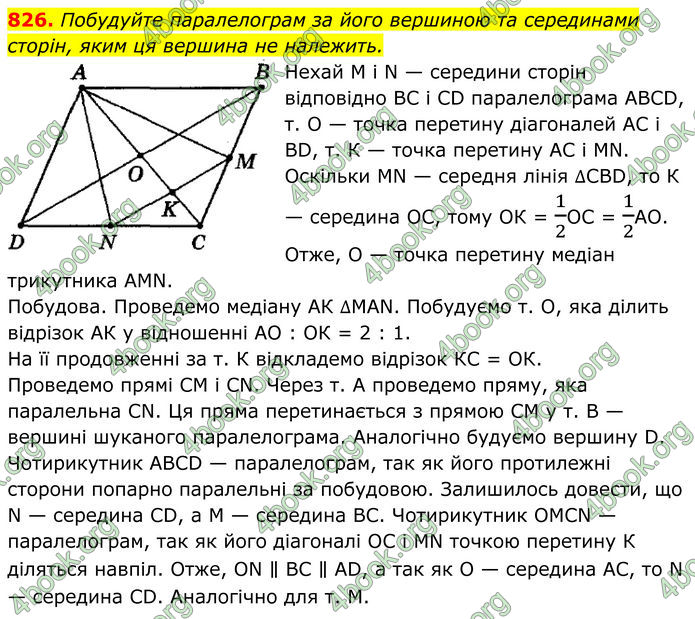
Побудуйте паралелограм за його вершиною та серединами сторін, яким ця вершина не належить.

Нехай М і N — середини сторін відповідно ВС і CD паралелограма ABCD, т. О — точка перетину діагоналей АС і BD, т. К — точка перетину АС і MN.
Оскільки MN — середня лінія ∆CBD, то К — середина ОС, тому ОК = 1/2ОС = 1/2АО. Отже, О — точка перетину медіан трикутника AMN.
Побудова. Проведемо медіану АК ∆MAN. Побудуємо т. О, яка ділить відрізок АК у відношенні АО : ОК = 2 : 1. На її продовженні за т. К відкладемо відрізок КС = ОК.
Проведемо прямі СМ і CN. Через т. А проведемо пряму, яка паралельна CN. Ця пряма перетинається з прямою СМ у т. В — вершині шуканого паралелограма.
Аналогічно будуємо вершину D. Чотирикутник ABCD — паралелограм, так як його протилежні сторони попарно паралельні за побудовою.
Залишилось довести, що N — середина CD, а М — середина ВС.
Чотирикутник OMCN — паралелограм, так як його діагоналі ОС і MN точкою перетину К діляться навпіл.
Отже, ON ∥ ВС ∥ AD, а так як О — середина АС, то N — середина CD. Аналогічно для т. М.