ГДЗ Геометрія 8 клас Бурда (2025)

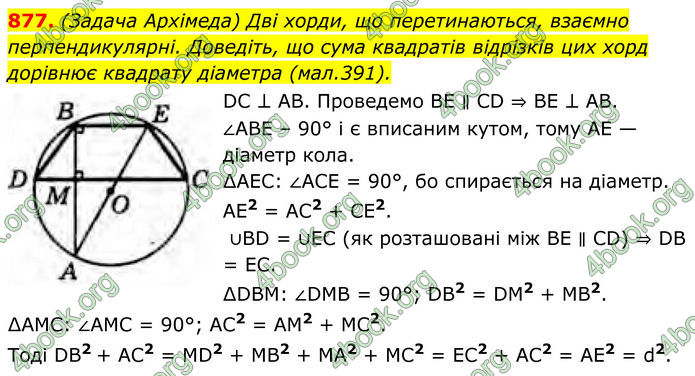
877. (Задача Архімеда) Дві хорди, що перетинаються, взаємно перпендикулярні. Доведіть, що сума квадратів відрізків цих хорд дорівнює квадрату діаметра (мал.391).

DC ⊥ AB. Проведемо BE ∥ CD ⇒ BE ⊥ АВ.
∠ABE – 90° і є вписаним кутом, тому АЕ — діаметр кола.
∆АЕС: ∠ACE = 90°, бо спирається на діаметр.
АЕ2 = АС2 + СE2. ∪BD = ∪EC (як розташовані між BE ∥ CD) ⇒ DB = EC.
∆DBM: ∠DMB = 90°; DB2 = DM2 + MB2.
∆AMC: ∠AMC = 90°; AC2 = AM2 + MC2.
Тоді DB2 + AC2 = MD2 + MB2 + MA2 + MC2 = EC2 + AC2 = AE2 = d2.