ГДЗ Геометрія 8 клас Бурда (2025)

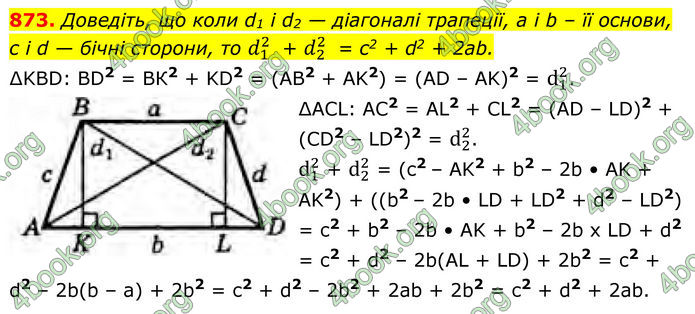
873. Доведіть, що коли d1 і d2 — діагоналі трапеції, a і b – її основи, с і d — бічні сторони, то d_1^2 + d_2^2 = с2 + d2 + 2аb.

∆KBD: BD2 = ВК2 + KD2 = (АВ2 + AK2) = (AD – AK)2 = d_1^2.
∆ACL: AC2 = AL2 + CL2 = (АD – LD)2 + (CD2 – LD2)2 = d_2^2.
d_1^2 + d_2^2 = (c2 – AK2 + b2 – 2b • AK + AK2) + ((b2 – 2b • LD + LD2 + d2 – LD2) = c2 + b2 – 2b • AK + b2 – 2b x LD + d2 = c2 + d2 – 2b(AL + LD) + 2b2 = c2 + d2 – 2b(b – a) + 2b2 = c2 + d2 – 2b2 + 2ab + 2b2 = c2 + d2 + 2ab.