ГДЗ Геометрія 8 клас Мерзляк (2025)

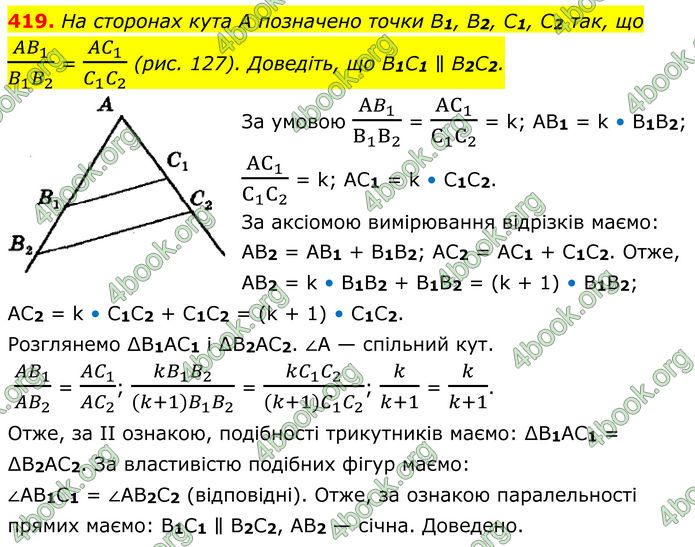
На сторонах кута А позначено точки B1, B2, C1, C2 так, що (AB_1)/(B_1 B_2 ) = (AC_1)/(C_1 C_2 ) (рис. 127). Доведіть, що B1C1 ∥ B2C2.

За умовою (AB_1)/(B_1 B_2 ) = (AC_1)/(C_1 C_2 ) = k; AB1 = k • B1B2; (AC_1)/(C_1 C_2 ) = k; АС1 = k • С1С2. За аксіомою вимірювання відрізків маємо: АВ2 = АВ1 + В1В2; АС2 = АС1 + С1С2. Отже, АВ2 = k • В1В2 + В1В2 = (k + 1) • В1В2; АС2 = k • С1С2 + С1С2 = (k + 1) • С1С2. Розглянемо ∆В1АС1 і ∆В2АС2. ∠А — спільний кут. (AB_1)/(AB_2 ) = (AC_1)/(AC_2 ); (kB_1 B_2)/((k+1)B_1 B_2 ) = (kC_1 C_2)/((k+1)C_1 C_2 ); k/(k+1) = k/(k+1). Отже, за II ознакою, подібності трикутників маємо: ∆В1АС1 = ∆В2АС2. За властивістю подібних фігур маємо: ∠АВ1С1 = ∠АВ2С2 (відповідні). Отже, за ознакою паралельності прямих маємо: В1С1 ∥ В2С2, АВ2 — січна. Доведено.