ГДЗ Геометрія 8 клас Мерзляк (2025)

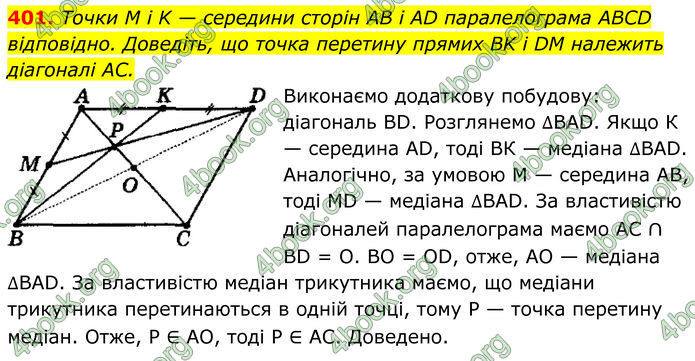
Точки M i K — середини сторін AB і AD паралелограма ABCD відповідно. Доведіть, що точка перетину прямих BK і DM належить діагоналі AC.

Виконаємо додаткову побудову: діагональ BD. Розглянемо ∆BАD.
Якщо К — середина АD, тоді ВК — медіана ∆ВАD. Аналогічно, за умовою М — середина АВ, тоді MD — медіана ∆ВАD.
За властивістю діагоналей паралелограма маємо АС ∩ ВD = О. ВО = ОD, отже, АО — медіана ∆ВАD.
За властивістю медіан трикутника маємо, що медіани трикутника перетинаються в одній точці, тому Р — точка перетину медіан. Отже, Р ∈ АО, тоді Р ∈ АС. Доведено.