ГДЗ Геометрія 8 клас Мерзляк (2025)

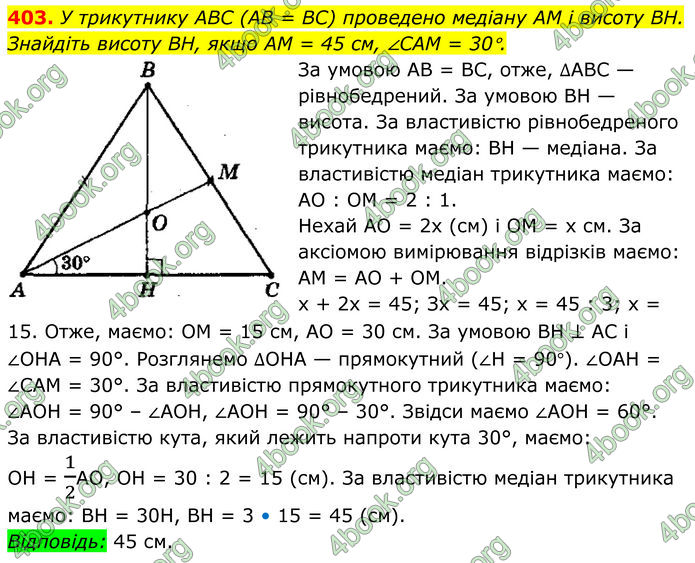
У трикутнику ABC (AB = BC) проведено медіану AM і висоту BH. Знайдіть висоту BH, якщо AM = 45 см, ∠CAM = 30°.

За умовою АВ = ВС, отже, ∆АВС — рівнобедрений. За умовою ВН — висота.
За властивістю рівнобедреного трикутника маємо: ВН — медіана.
За властивістю медіан трикутника маємо: АО : ОМ = 2 : 1.
Нехай АО = 2х (см) і ОМ = х см. За аксіомою вимірювання відрізків маємо: АМ = АО + ОМ. х + 2х = 45; Зх = 45; х = 45 : 3; х = 15.
Отже, маємо: ОМ = 15 см, АО = 30 см. За умовою ВН ⊥ АС і ∠ОНА = 90°.
Розглянемо ∆OНА — прямокутний (∠Н = 90°). ∠ОАН = ∠САМ = 30°.
За властивістю прямокутного трикутника маємо: ∠АОН = 90° – ∠АОН, ∠АОН = 90° – 30°.
Звідси маємо ∠АОН = 60°. За властивістю кута, який лежить напроти кута 30°, маємо: ОН = 1/2АО, OH = 30 : 2 = 15 (см).
За властивістю медіан трикутника маємо: ВН = 30Н, ВН = 3 • 15 = 45 (см).
Відповідь: 45 см.