ГДЗ Геометрія 8 клас Мерзляк (2025)

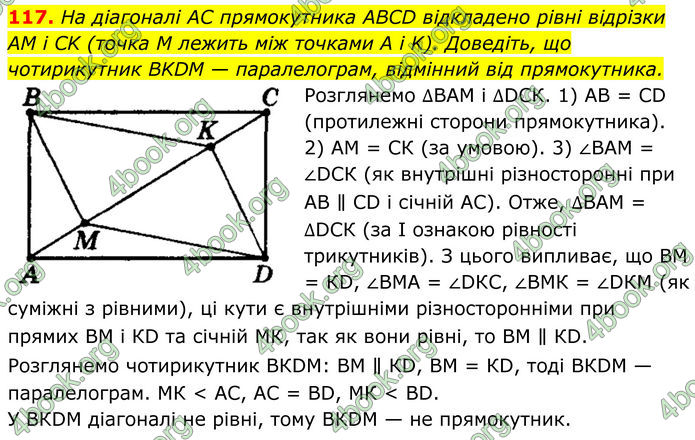
На діагоналі AC прямокутника ABCD відкладено рівні відрізки AM і CK (точка M лежить між точками А і K). Доведіть, що чотирикутник BKDM — паралелограм, відмінний від прямокутника.

Розглянемо ∆ВАМ і ∆DСК. 1) АВ = СD (протилежні сторони прямокутника). 2) АМ = СК (за умовою). 3) ∠ВАМ = ∠DСК (як внутрішні різносторонні при АВ ∥ СD і січній АС). Отже, ∆ВАМ = ∆DСК (за І ознакою рівності трикутників). З цього випливає, що ВМ = КD, ∠ВМА = ∠DКС, ∠ВМК = ∠DКМ (як суміжні з рівними), ці кути є внутрішніми різносторонніми при прямих ВМ і КD та січній МК, так як вони рівні, то ВМ ∥ КD. Розглянемо чотирикутник ВКDМ: ВМ ∥ КD, ВМ = КD, тоді ВКDМ — паралелограм. МК < АС, АС = ВD, МК < ВD. У ВКDМ діагоналі не рівні, тому ВКDМ — не прямокутник.