ГДЗ Геометрія 8 клас Мерзляк (2025)

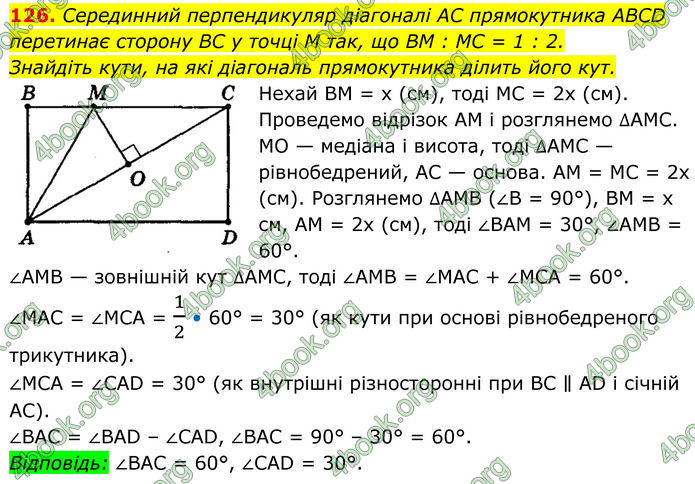
Серединний перпендикуляр діагоналі AC прямокутника ABCD перетинає сторону BC у точці M так, що BM : MC = 1 : 2. Знайдіть кути, на які діагональ прямокутника ділить його кут.

Нехай ВМ = х (см), тоді МС = 2х (см). Проведемо відрізок АМ і розглянемо ∆АМС. МО — медіана і висота, тоді ∆АМС — рівнобедрений, АС — основа. АМ = МС = 2х (см).
Розглянемо ∆АМВ (∠В = 90°), ВМ = х см, АМ = 2х (см), тоді ∠ВАМ = 30°, ∠АМВ = 60°.
∠АМВ — зовнішній кут ∆АМС, тоді ∠АМВ = ∠МАС + ∠МСА = 60°. ∠MAC = ∠MCA = 1/2 • 60° = 30° (як кути при основі рівнобедреного трикутника).
∠МСА = ∠CAD = 30° (як внутрішні різносторонні при ВС ∥ AD і січній АС). ∠ВАС = ∠BAD – ∠CAD, ∠ВАС = 90° – 30° = 60°.
Відповідь: ∠ВАС = 60°, ∠CAD = 30°.