ГДЗ Геометрія 8 клас Мерзляк (2025)

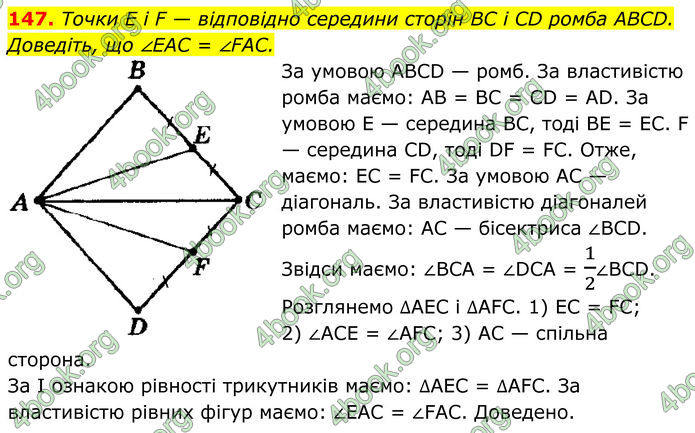
Точки E i F — відповідно середини сторін BC і CD ромба ABCD. Доведіть, що ∠EAC = ∠FAC.

За умовою АВСD — ромб. За властивістю ромба маємо: АВ = ВС = СD = АD.
За умовою Е — середина ВС, тоді ВЕ = ЕС. F — середина СD, тоді DF = FС.
Отже, маємо: ЕС = FС. За умовою АС — діагональ.
За властивістю діагоналей ромба маємо: АС — бісектриса ∠ВСD. Звідси маємо: ∠BCA = ∠DCA = 1/2∠BCD.
Розглянемо ∆АЕС і ∆АFС. 1) ЕС = FС; 2) ∠АСЕ = ∠АFС; 3) АС — спільна сторона. За І ознакою рівності трикутників маємо: ∆АЕС = ∆AFC.
За властивістю рівних фігур маємо: ∠ЕАС = ∠FАС. Доведено.