ГДЗ Геометрія 7 клас Мерзляк (2024)

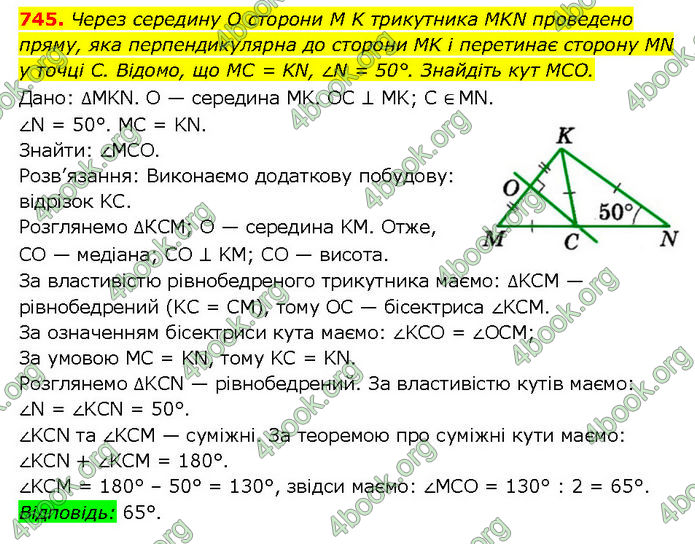
Через середину O сторони M K трикутника MKN проведено пряму, яка перпендикулярна до сторони MK і перетинає сторону MN у точці С. Відомо, що MC = KN, ∠N = 50°. Знайдіть кут MCO.

Дано: ∆MKN. O — середина MK. OC ⊥ MK; C ∈ MN. ∠N = 50°. MC = KN. Знайти: ∠MCO. Розв’язання: Виконаємо додаткову побудову: відрізок KC. Розглянемо ∆КСМ; O — середина KM. Отже, CO — медіана; CO ⊥ KM; CO — висота. За властивістю рівнобедреного трикутника маємо: ∆KCM — рівнобедрений (KC = CM), тому OC — бісектриса ∠KCM. За означенням бісектриси кута маємо: ∠KCO = ∠OCM; За умовою MC = KN, тому KC = KN. Розглянемо ∆KCN — рівнобедрений. За властивістю кутів маємо: ∠N = ∠KCN = 50°. ∠KCN та ∠KCM — суміжні. За теоремою про суміжні кути маємо: ∠KCN + ∠KCM = 180°. ∠KCM = 180° – 50° = 130°, звідси маємо: ∠MCO = 130° : 2 = 65°. ЭВідповідь: 65°.