ГДЗ Геометрія 8 клас Бевз (2025)

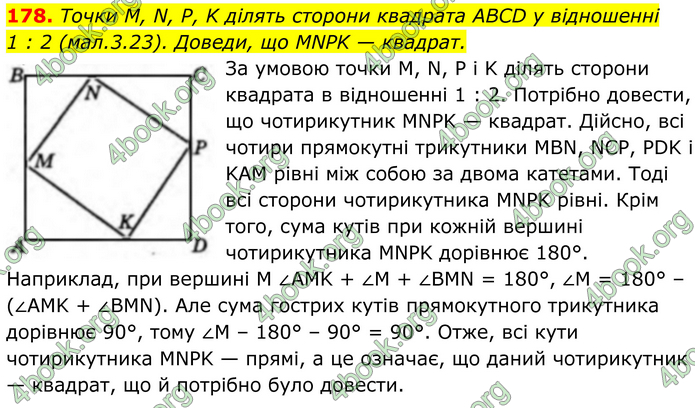
Точки M, N, P, K ділять сторони квадрата ABCD у відношенні 1 : 2 (мал.3.23). Доведи, що MNPK — квадрат.

За умовою точки М, N, P і K ділять сторони квадрата в відношенні 1 : 2. Потрібно довести, що чотирикутник MNPK — квадрат. Дійсно, всі чотири прямокутні трикутники MBN, NCP, PDK і KAM рівні між собою за двома катетами. Тоді всі сторони чотирикутника MNPK рівні. Крім того, сума кутів при кожній вершині чотирикутника MNPK дорівнює 180°. Наприклад, при вершині M ∠AMK + ∠M + ∠BMN = 180°, ∠M = 180° – (∠AMK + ∠BMN). Але сума гострих кутів прямокутного трикутника дорівнює 90°, тому ∠M – 180° – 90° = 90°. Отже, всі кути чотирикутника MNPK — прямі, а це означає, що даний чотирикутник — квадрат, що й потрібно було довести.