ГДЗ Геометрія 8 клас Бевз (2025)

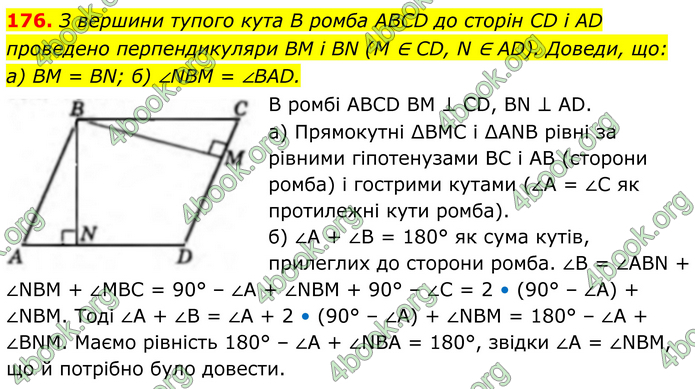
З вершини тупого кута B ромба ABCD до сторін CD і AD проведено перпендикуляри BM і BN (M ∈ CD, N ∈ AD). Доведи, що: а) BM = BN; б) ∠NBM = ∠BAD.

В ромбі ABCD BM ⊥ CD, BN ⊥ AD. а) Прямокутні ∆BMC і ∆ANB рівні за рівними гіпотенузами BC і AB (сторони ромба) і гострими кутами (∠А = ∠C як протилежні кути ромба). б) ∠A + ∠B = 180° як сума кутів, прилеглих до сторони ромба. ∠B = ∠ABN + ∠NBM + ∠MBC = 90° – ∠A + ∠NBM + 90° – ∠C = 2 • (90° – ∠A) + ∠NBM. Тоді ∠A + ∠B = ∠A + 2 • (90° – ∠A) + ∠NBM = 180° – ∠A + ∠BNM. Маємо рівність 180° – ∠A + ∠NBA = 180°, звідки ∠A = ∠NBM, що й потрібно було довести.