ГДЗ Геометрія 8 клас Бевз (2025)

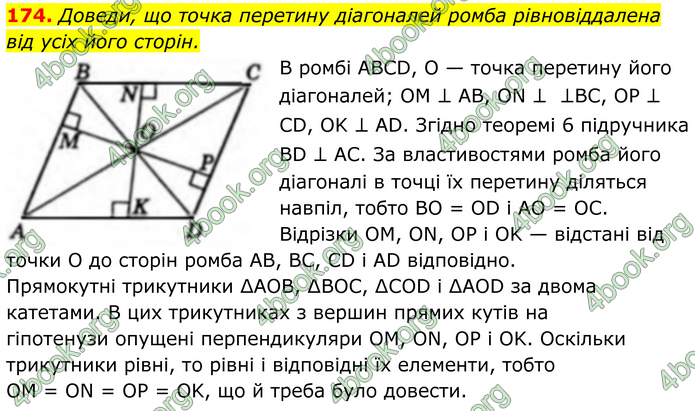
Доведи, що точка перетину діагоналей ромба рівновіддалена від усіх його сторін.

В ромбі ABCD, O — точка перетину його діагоналей; OM ⊥ AB, ON ⊥ ⊥BC, OP ⊥ CD, OK ⊥ AD. Згідно теоремі 6 підручника BD ⊥ AC. За властивостями ромба його діагоналі в точці їх перетину діляться навпіл, тобто BO = OD і AO = ОС. Відрізки ОМ, ON, OP і OK — відстані від точки O до сторін ромба AВ, BC, CD і AD відповідно. Прямокутні трикутники ∆АОВ, ∆BOC, ∆COD і ∆AOD за двома катетами. В цих трикутниках з вершин прямих кутів на гіпотенузи опущені перпендикуляри ОМ, ON, OP і OK. Оскільки трикутники рівні, то рівні і відповідні їх елементи, тобто OM = ON = OP = OK, що й треба було довести.