ГДЗ Геометрія 8 клас Бевз (2025)

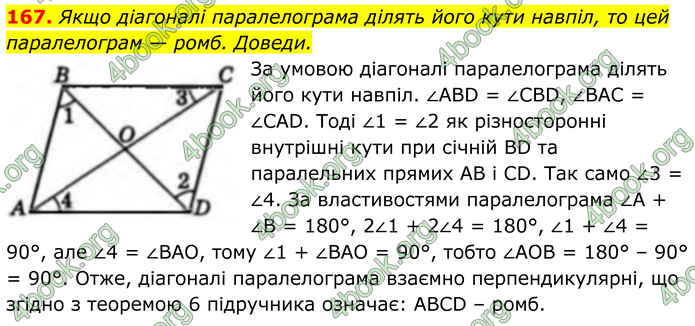
Якщо діагоналі паралелограма ділять його кути навпіл, то цей паралелограм — ромб. Доведи.

За умовою діагоналі паралелограма ділять його кути навпіл. ∠ABD = ∠CBD, ∠BAC = ∠CAD. Тоді ∠1 = ∠2 як різносторонні внутрішні кути при січній BD та паралельних прямих AB і CD. Так само ∠3 = ∠4. За властивостями паралелограма ∠A + ∠B = 180°, 2∠1 + 2∠4 = 180°, ∠1 + ∠4 = 90°, але ∠4 = ∠BAO, тому ∠1 + ∠BAO = 90°, тобто ∠AOB = 180° – 90° = 90°. Отже, діагоналі паралелограма взаємно перпендикулярні, що згідно з теоремою 6 підручника означає: ABCD – ромб.