Назад
ГДЗ Геометрія 8 клас Бурда (2025)
Реклама:
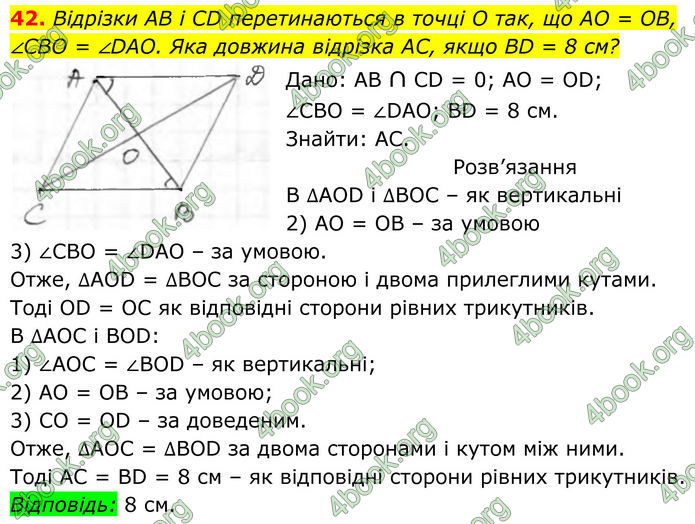
42. Відрізки AB і CD перетинаються в точці O так, що AO = OB, ∠CBO = ∠DAO. Яка довжина відрізка AC, якщо BD = 8 см?
Дано: АВ ∩ CD = 0; AO = OD; ∠CBO = ∠DAO; BD = 8 см. Знайти: АС.
Розв’язання
В ∆AOD і ∆ВОС – як вертикальні
2) АО = ОВ – за умовою
3) ∠СВО = ∠DAO – за умовою. Отже, ∆AOD = ∆BOC за стороною і двома прилеглими кутами.
Тоді OD = OC як відповідні сторони рівних трикутників.
В ∆АОС і BOD: 1) ∠АОС = ∠BOD – як вертикальні;
2) АО = ОВ – за умовою; 3) СО = OD – за доведеним. Отже, ∆АОС = ∆BOD за двома сторонами і кутом між ними.
Тоді АС = BD = 8 см – як відповідні сторони рівних трикутників.
Відповідь: 8 см.
Дано: АВ ∩ CD = 0; AO = OD; ∠CBO = ∠DAO; BD = 8 см. Знайти: АС.
Розв’язання
В ∆AOD і ∆ВОС – як вертикальні
2) АО = ОВ – за умовою
3) ∠СВО = ∠DAO – за умовою. Отже, ∆AOD = ∆BOC за стороною і двома прилеглими кутами.
Тоді OD = OC як відповідні сторони рівних трикутників.
В ∆АОС і BOD: 1) ∠АОС = ∠BOD – як вертикальні;
2) АО = ОВ – за умовою; 3) СО = OD – за доведеним. Отже, ∆АОС = ∆BOD за двома сторонами і кутом між ними.
Тоді АС = BD = 8 см – як відповідні сторони рівних трикутників.
Відповідь: 8 см.






