ГДЗ Геометрія 8 клас Мерзляк (2025)

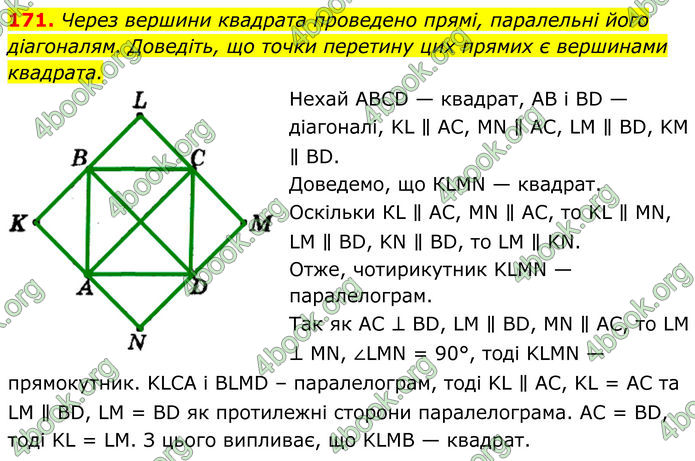
Через вершини квадрата проведено прямі, паралельні його діагоналям. Доведіть, що точки перетину цих прямих є вершинами квадрата.

Нехай АВСD — квадрат, АВ і ВD — діагоналі, KL ∥ АС, МN ∥ АС, LМ ∥ ВD, KM ∥ ВD. Доведемо, що КLМN — квадрат. Оскільки КL ∥ АС, МN ∥ АС, то KL ∥ МN, LM ∥ ВD, KN ∥ ВD, то LM ∥ KN. Отже, чотирикутник KLМN — паралелограм. Так як АС ⊥ ВD, LМ ∥ ВD, МN ∥ АС, то LМ ⊥ МN, ∠LМN = 90°, тоді KLМN — прямокутник. KLСА і BLMD – паралелограм, тоді KL ∥ АС, KL = АС та LМ ∥ ВD, LМ = ВD як протилежні сторони паралелограма. АС = ВD, тоді KL = LМ. З цього випливає, що KLМB — квадрат.