ГДЗ Геометрія 8 клас Мерзляк (2025)

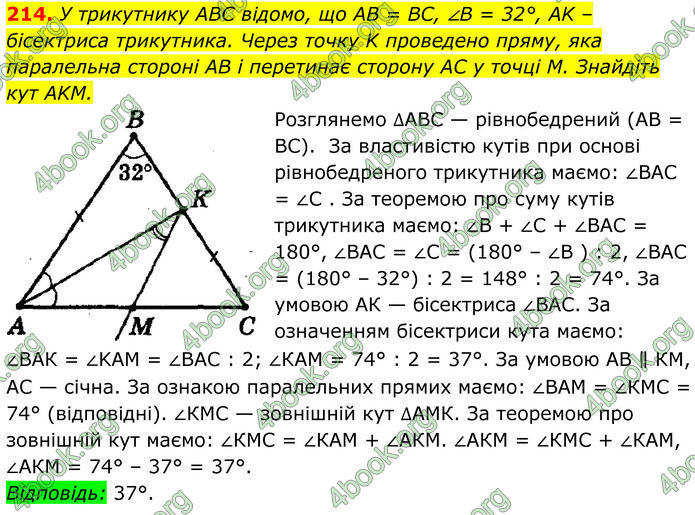
У трикутнику ABC відомо, що AB = BC, ∠B = 32°, AK –бісектриса трикутника. Через точку K проведено пряму, яка паралельна стороні AB і перетинає сторону AC у точці М. Знайдіть кут AKM.

Розглянемо ∆ABC — рівнобедрений (АВ = ВС). За властивістю кутів при основі рівнобедреного трикутника маємо: ∠ВАС = ∠С . За теоремою про суму кутів трикутника маємо: ∠В + ∠С + ∠ВАС = 180°, ∠ВАС = ∠С = (180° – ∠В ) : 2, ∠ВАС = (180° – 32°) : 2 = 148° : 2 = 74°. За умовою АК — бісектриса ∠ВАС. За означенням бісектриси кута маємо: ∠ВАК = ∠KАМ = ∠ВАС : 2; ∠КАМ = 74° : 2 = 37°. За умовою АВ ∥ КМ, АС — січна. За ознакою паралельних прямих маємо: ∠ВАМ = ∠КМС = 74° (відповідні). ∠КМС — зовнішній кут ∆АМК. За теоремою про зовнішній кут маємо: ∠КМС = ∠КАМ + ∠АКМ. ∠АКМ = ∠КМС + ∠КАМ, ∠АКМ = 74° – 37° = 37°.
Відповідь: 37°.