ГДЗ Геометрія 8 клас Мерзляк (2025)

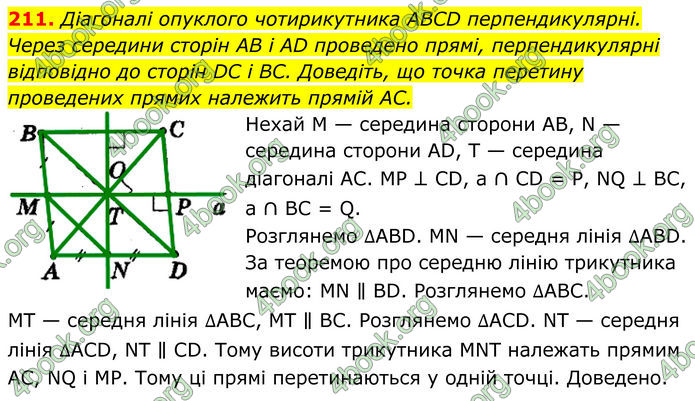
Діагоналі опуклого чотирикутника ABCD перпендикулярні. Через середини сторін AB і AD проведено прямі, перпендикулярні відповідно до сторін DC і BC. Доведіть, що точка перетину проведених прямих належить прямій AC.

Нехай М — середина сторони АВ, N — середина сторони АD, Т — середина діагоналі АС. МР ⊥ СD, а ∩ СD = Р, NQ ⊥ ВС, а ∩ ВС = Q. Розглянемо ∆АBD. МN — середня лінія ∆АВD. За теоремою про середню лінію трикутника маємо: МN ∥ ВD. Розглянемо ∆АВС. МТ — середня лінія ∆АВС, МТ ∥ ВС. Розглянемо ∆АСD. NТ — середня лінія ∆АСD, NТ ∥ СD. Тому висоти трикутника МNТ належать прямим АС, NQ і МР. Тому ці прямі перетинаються у одній точці. Доведено.