ГДЗ Геометрія 8 клас Мерзляк (2025)

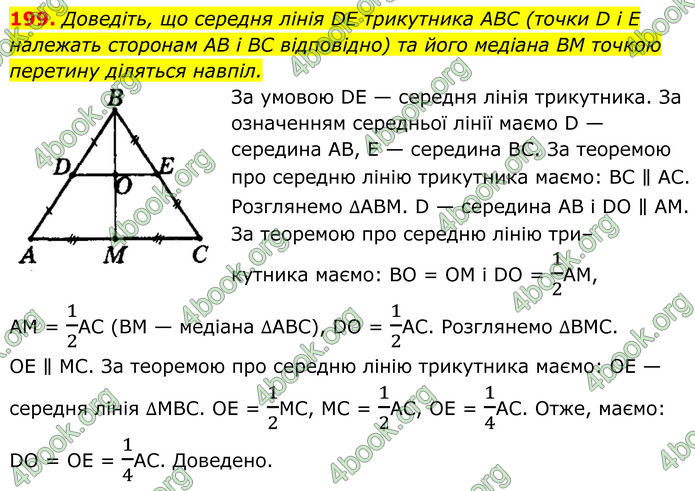
Доведіть, що середня лінія DE трикутника ABC (точки D і E належать сторонам AB і BC відповідно) та його медіана BM точкою перетину діляться навпіл.

За умовою DE — середня лінія трикутника. За означенням середньої лінії маємо D — середина АВ, Е — середина ВС. За теоремою про середню лінію трикутника маємо: BC ∥ АС. Розглянемо ∆АВМ. D — середина АВ і DО ∥ АМ. За теоремою про середню лінію три– кутника маємо: ВО = ОМ і DО = 1/2АМ, АМ = 1/2АС (ВМ — медіана ∆АВС), DО = 1/2АС. Розглянемо ∆ВМС. ОЕ ∥ МС. За теоремою про середню лінію трикутника маємо: ОЕ — середня лінія ∆МВС. ОЕ = 1/2МС, МС = 1/2АС, ОЕ = 1/4АС. Отже, маємо: DО = ОЕ = 1/4АС. Доведено.