ГДЗ Геометрія 8 клас Мерзляк (2025)

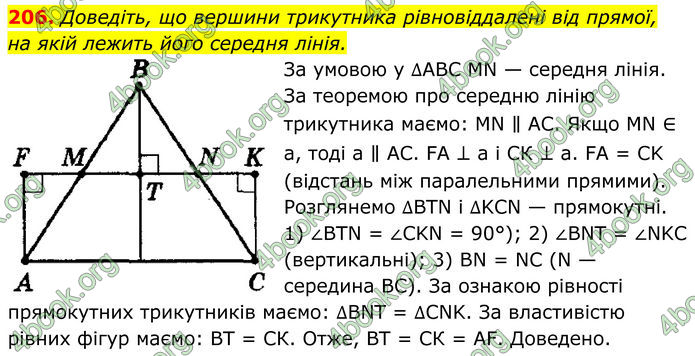
Доведіть, що вершини трикутника рівновіддалені від прямої, на якій лежить його середня лінія. За умовою у ∆АВС МN — середня лінія.

За теоремою про середню лінію трикутника маємо: МN ∥ АС. Якщо МN ∈ а, тоді а ∥ АС. FА ⊥ а і СК ⊥ а. FА = СK (відстань між паралельними прямими). Розглянемо ∆ВТN і ∆KСN — прямокутні. 1) ∠ВTN = ∠CKN = 90°); 2) ∠ВNТ = ∠NKС (вертикальні); 3) ВN = NС (N — середина ВС). За ознакою рівності прямокутних трикутників маємо: ∆BNT = ∆СNK. За властивістю рівних фігур маємо: ВТ = СК. Отже, ВТ = СК = АF. Доведено.