ГДЗ Геометрія 8 клас Мерзляк (2025)

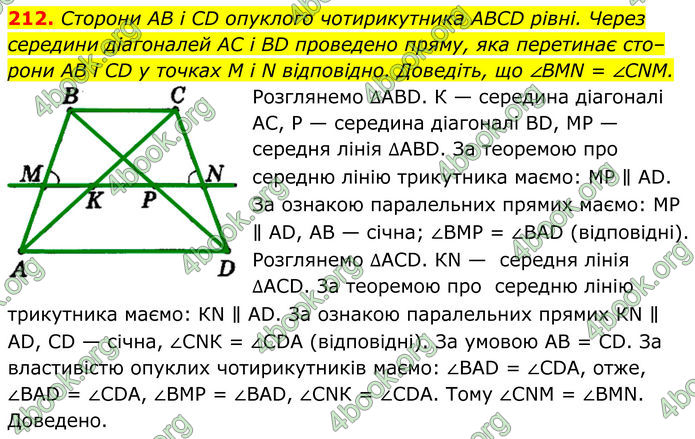
Сторони AB і CD опуклого чотирикутника ABCD рівні. Через середини діагоналей AC і BD проведено пряму, яка перетинає сто–рони AB і CD у точках M і N відповідно. Доведіть, що ∠BMN = ∠CNM.

Розглянемо ∆АВD. К — середина діагоналі АС, Р — середина діагоналі ВD, МР — середня лінія ∆АВD. За теоремою про середню лінію трикутника маємо: МР ∥ АD. За ознакою паралельних прямих маємо: МР ∥ АD, АВ — січна; ∠ВМР = ∠ВАD (відповідні). Розглянемо ∆АСD. КN — середня лінія ∆АСD. За теоремою про середню лінію трикутника маємо: КN ∥ АD. За ознакою паралельних прямих КN ∥ АD, СD — січна, ∠СNК = ∠СDА (відповідні). За умовою АВ = СD. За властивістю опуклих чотирикутників маємо: ∠ВАD = ∠СDА, отже, ∠ВАD = ∠СDА, ∠ВМР = ∠ВАD, ∠СNК = ∠СDА. Тому ∠СNМ = ∠ВМN. Доведено.