ГДЗ Геометрія 8 клас Мерзляк (2025)

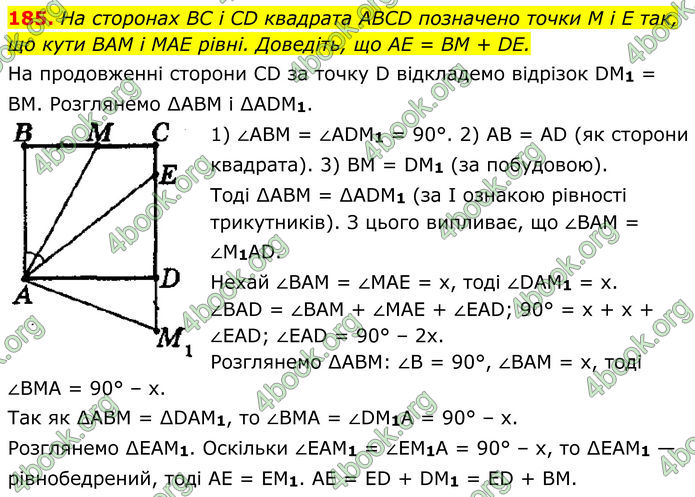
На сторонах BC і CD квадрата ABCD позначено точки M і E так, що кути ВАМ і MAE рівні. Доведіть, що AE = BM + DE.

На продовженні сторони СD за точку D відкладемо відрізок DМ1 = ВМ. Розглянемо ∆АВМ і ∆АDM1. 1) ∠АВМ = ∠АDМ1 = 90°. 2) АВ = АD (як сторони квадрата). 3) ВМ = DМ1 (за побудовою). Тоді ∆АВМ = ∆АDM1 (за І ознакою рівності трикутників). З цього випливає, що ∠ВАМ = ∠М1АD. Нехай ∠ВАМ = ∠МАЕ = х, тоді ∠DАМ1 = х. ∠ВАD = ∠ВАМ + ∠МАЕ + ∠ЕАD; 90° = х + х + ∠ЕАD; ∠ЕАD = 90° – 2x. Розглянемо ∆АВМ: ∠В = 90°, ∠ВАМ = х, тоді ∠ВМА = 90° – х. Так як ∆АВМ = ∆DAM1, то ∠ВМА = ∠DМ1А = 90° – х. Розглянемо ∆ЕАМ1. Оскільки ∠ЕАМ1 = ∠ЕМ1А = 90° – х, то ∆ЕАМ1 — рівнобедрений, тоді АЕ = ЕМ1. АЕ = ЕD + DМ1 = ЕD + ВМ.