ГДЗ Геометрія 8 клас Мерзляк (2025)

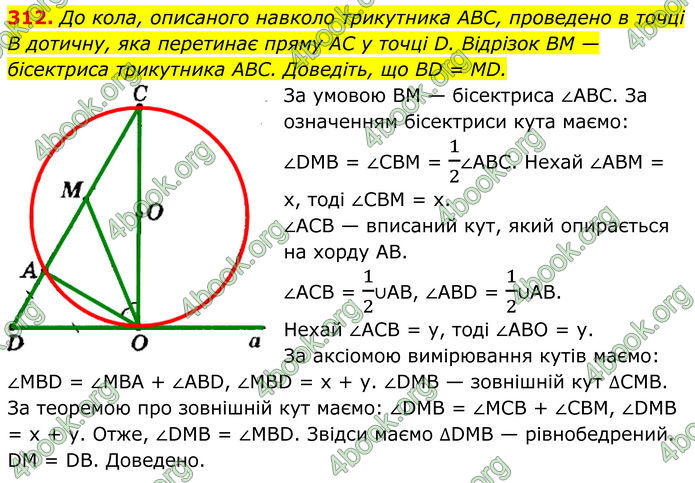
До кола, описаного навколо трикутника ABC, проведено в точці В дотичну, яка перетинає пряму AC у точці D. Відрізок BM — бісектриса трикутника ABC. Доведіть, що BD = MD.

За умовою ВМ — бісектриса ∠ABC. За означенням бісектриси кута маємо: ∠DMB = ∠CBM = 1/2∠ABC.
Нехай ∠АВМ = х, тоді ∠CBM = х. ∠АСВ — вписаний кут, який опирається на хорду AB.
∠АСВ = 1/2∪АВ, ∠ABD = 1/2∪АВ. Нехай ∠АСВ = у, тоді ∠АВО = у.
За аксіомою вимірювання кутів маємо: ∠МВD = ∠МВА + ∠ABD, ∠МВD = х + у.
∠DМВ — зовнішній кут ∆СМВ. За теоремою про зовнішній кут маємо: ∠DМВ = ∠МСВ + ∠СВМ, ∠DМВ = х + у.
Отже, ∠DМВ = ∠МВD. Звідси маємо ∆DМВ — рівнобедрений. DМ = DВ. Доведено.