ГДЗ Геометрія 8 клас Мерзляк (2025)

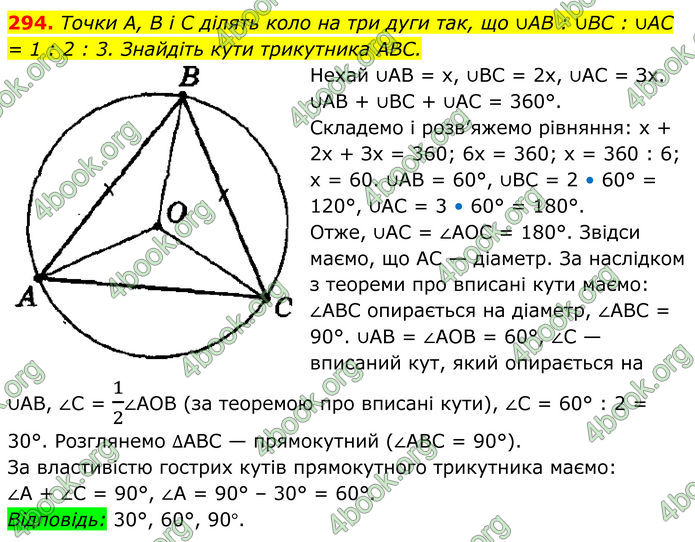
Точки А, В і C ділять коло на три дуги так, що ∪AB : ∪BC : ∪AC = 1 : 2 : 3. Знайдіть кути трикутника ABC.

Нехай ∪АВ = х, ∪ВС = 2х, ∪АС = Зх. ∪АВ + ∪ВС + ∪АС = 360°.
Складемо і розв’яжемо рівняння: х + 2х + Зх = 360; 6x = 360; x = 360 : 6; x = 60. ∪АВ = 60°, ∪ВС = 2 • 60° = 120°, ∪АС = 3 • 60° = 180°.
Отже, ∪АС = ∠АОС = 180°. Звідси маємо, що АС — діаметр.
За наслідком з теореми про вписані кути маємо: ∠АВС опирається на діаметр, ∠АВС = 90°. ∪AB = ∠АОВ = 60°, ∠С — вписаний кут, який опирається на ∪АВ, ∠С = 1/2∠АОВ (за теоремою про вписані кути), ∠С = 60° : 2 = 30°.
Розглянемо ∆АВС — прямокутний (∠АВС = 90°).
За властивістю гострих кутів прямокутного трикутника маємо: ∠А + ∠С = 90°, ∠А = 90° – 30° = 60°.
Відповідь: 30°, 60°, 90°.