ГДЗ Геометрія 8 клас Бевз (2025)

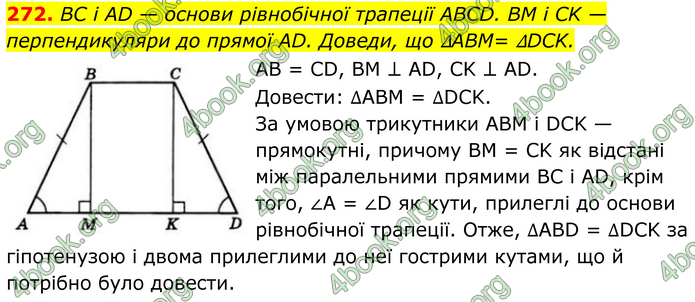
BC і AD — основи рівнобічної трапеції ABCD. BM і CK — перпендикуляри до прямої AD. Доведи, що ∆ABM= ∆DCK. AB = CD, BM ⊥ AD, CK ⊥ AD. Довести: ∆ABM = ∆DCK.

За умовою трикутники ABM і DCK — прямокутні, причому BM = CK як відстані між паралельними прямими BC і AD, крім того, ∠A = ∠D як кути, прилеглі до основи рівнобічної трапеції. Отже, ∆ABD = ∆DCK за гіпотенузою і двома прилеглими до неї гострими кутами, що й потрібно було довести.