ГДЗ Геометрія 8 клас Бевз (2025)

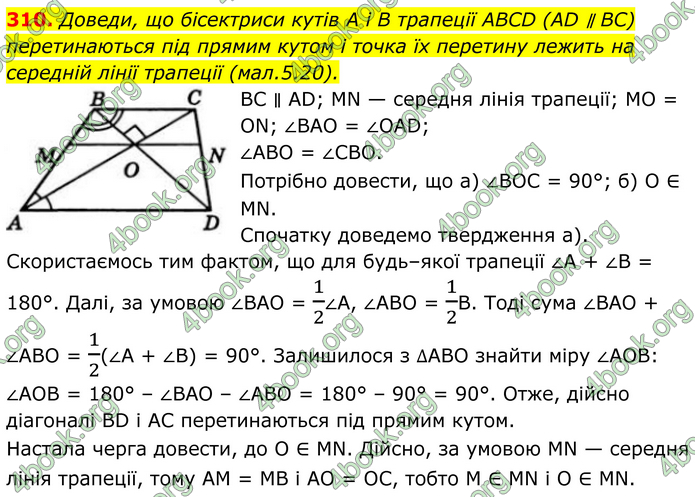
Доведи, що бісектриси кутів A і B трапеції ABCD (AD ∥ BC) перетинаються під прямим кутом і точка їх перетину лежить на середній лінії трапеції (мал.5.20).

BC ∥ AD; MN — середня лінія трапеції; MO = ON; ∠BAO = ∠OAD; ∠ABO = ∠CBO. Потрібно довести, що a) ∠BOC = 90°; б) O ∈ MN. Спочатку доведемо твердження а). Скористаємось тим фактом, що для будь–якої трапеції ∠A + ∠B = 180°. Далі, за умовою ∠BAO = 1/2∠A, ∠ABO = 1/2B. Тоді сума ∠BAO + ∠ABO = 1/2(∠A + ∠B) = 90°. Залишилося з ∆АВО знайти міру ∠AOВ: ∠AOB = 180° – ∠BAO – ∠ABO = 180° – 90° = 90°. Отже, дійсно діагоналі BD і AC перетинаються під прямим кутом. Настала черга довести, до O ∈ MN. Дійсно, за умовою MN — середня лінія трапеції, тому AM = MB і AO = ОС, тобто M ∈ MN і O ∈ MN.