ГДЗ Геометрія 8 клас Бевз (2025)

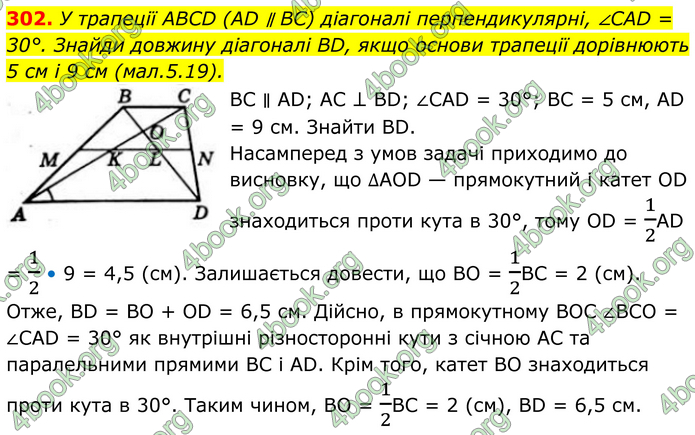
У трапеції ABCD (AD ∥ BC) діагоналі перпендикулярні, ∠CAD = 30°. Знайди довжину діагоналі BD, якщо основи трапеції дорівнюють 5 см і 9 см (мал.5.19).

BC ∥ AD; AC ⊥ BD; ∠CAD = 30°; BC = 5 см, AD = 9 см. Знайти BD. Насамперед з умов задачі приходимо до висновку, що ∆AOD — прямокутний і катет OD знаходиться проти кута в 30°, тому OD = 1/2AD = 1/2 • 9 = 4,5 (см). Залишається довести, що BO = 1/2BC = 2 (см). Отже, BD = BO + OD = 6,5 см. Дійсно, в прямокутному BOC ∠BCO = ∠CAD = 30° як внутрішні різносторонні кути з січною AC та паралельними прямими BC і AD. Крім того, катет BO знаходиться проти кута в 30°. Таким чином, BO = 1/2BC = 2 (см), BD = 6,5 см.