ГДЗ Геометрія 8 клас Бевз (2025)

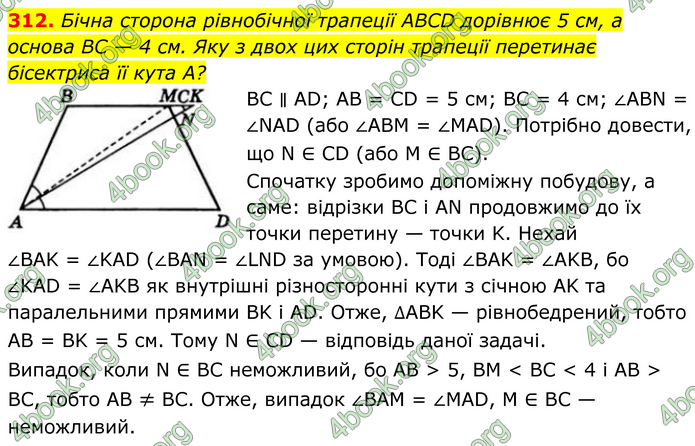
Бічна сторона рівнобічної трапеції ABCD дорівнює 5 см, а основа BC — 4 см. Яку з двох цих сторін трапеції перетинає бісектриса її кута A?

BC ∥ AD; AB = CD = 5 см; BC = 4 см; ∠ABN = ∠NAD (або ∠ABM = ∠MAD). Потрібно довести, що N ∈ CD (або M ∈ BC). Спочатку зробимо допоміжну побудову, а саме: відрізки BC і AN продовжимо до їх точки перетину — точки K. Нехай ∠BAK = ∠KAD (∠BAN = ∠LND за умовою). Тоді ∠BAK = ∠AKB, бо ∠KAD = ∠AKB як внутрішні різносторонні кути з січною AK та паралельними прямими BK і AD. Отже, ∆ABK — рівнобедрений, тобто AB = BK = 5 см. Тому N ∈ CD — відповідь даної задачі. Випадок, коли N ∈ BC неможливий, бо AB > 5, BM < BC < 4 і AB > BC, тобто AB ≠ BC. Отже, випадок ∠BAM = ∠MAD, M ∈ BC — неможливий.