ГДЗ Геометрія 8 клас Бевз (2025)

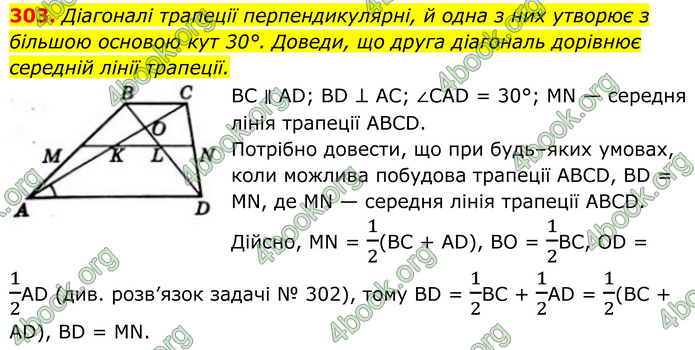
Діагоналі трапеції перпендикулярні, й одна з них утворює з більшою основою кут 30°. Доведи, що друга діагональ дорівнює середній лінії трапеції.

BC ∥ AD; BD ⊥ AC; ∠CAD = 30°; MN — середня лінія трапеції ABCD. Потрібно довести, що при будь–яких умовах, коли можлива побудова трапеції ABCD, BD = MN, де MN — середня лінія трапеції ABCD. Дійсно, MN = 1/2(BC + AD), BO = 1/2BC, OD = 1/2AD (див. розв’язок задачі № 302), тому BD = 1/2BC + 1/2AD = 1/2(BC + AD), BD = MN.