ГДЗ Геометрія 8 клас Бевз (2025)

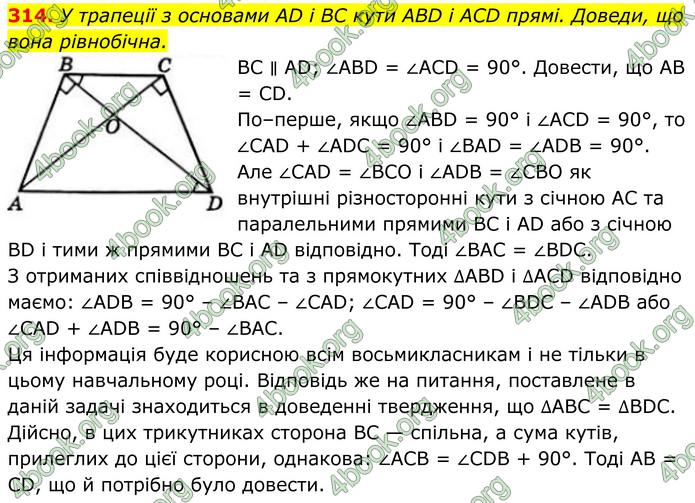
У трапеції з основами AD і BC кути ABD і ACD прямі. Доведи, що вона рівнобічна.

BC ∥ AD; ∠ABD = ∠ACD = 90°. Довести, що AB = CD. По–перше, якщо ∠ABD = 90° і ∠ACD = 90°, то ∠CAD + ∠ADC = 90° і ∠BAD = ∠ADB = 90°. Але ∠CAD = ∠BCO і ∠ADB = ∠CBO як внутрішні різносторонні кути з січною AC та паралельними прямими BC і AD або з січною BD і тими ж прямими BC і AD відповідно. Тоді ∠BAC = ∠BDC. З отриманих співвідношень та з прямокутних ∆ABD і ∆ACD відповідно маємо: ∠ADB = 90° – ∠BAC – ∠CAD; ∠CAD = 90° – ∠BDC – ∠ADB або ∠CAD + ∠ADB = 90° – ∠BAC. Ця інформація буде корисною всім восьмикласникам і не тільки в цьому навчальному році. Відповідь же на питання, поставлене в даній задачі знаходиться в доведенні твердження, що ∆ABC = ∆BDC. Дійсно, в цих трикутниках сторона BC — спільна, а сума кутів, прилеглих до цієї сторони, однакова: ∠ACB = ∠CDB + 90°. Тоді AB = CD, що й потрібно було довести.