ГДЗ Геометрія 8 клас Бевз (2025)

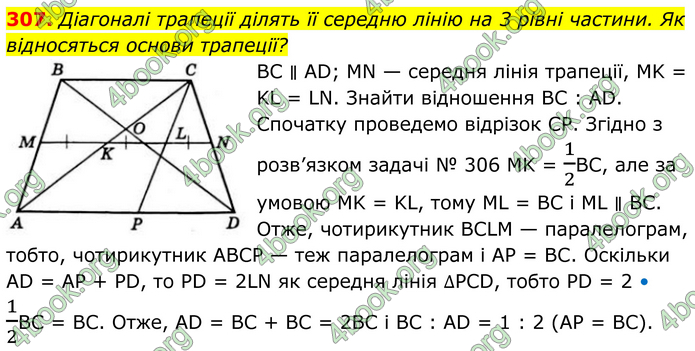
Діагоналі трапеції ділять її середню лінію на 3 рівні частини. Як відносяться основи трапеції?

BC ∥ AD; MN — середня лінія трапеції, MK = KL = LN. Знайти відношення BC : AD. Спочатку проведемо відрізок CP. Згідно з розв’язком задачі № 306 MK = 1/2BC, але за умовою MK = KL, тому ML = BC і ML ∥ ВС. Отже, чотирикутник BCLM — паралелограм, тобто, чотирикутник ABCP — теж паралелограм і AP = ВС. Оскільки AD = AP + PD, то PD = 2LN як середня лінія ∆PCD, тобто PD = 2 • 1/2ВC = ВС. Отже, AD = BC + BC = 2BC і BC : AD = 1 : 2 (АР = ВС).