ГДЗ Геометрія 8 клас Бевз (2025)

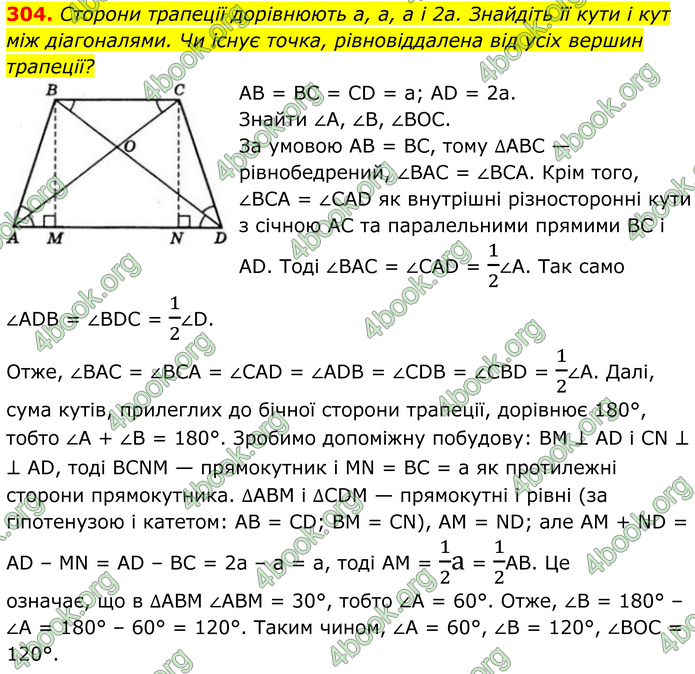
Сторони трапеції дорівнюють a, a, a і 2a. Знайдіть її кути і кут між діагоналями. Чи існує точка, рівновіддалена від усіх вершин трапеції?

AB = BC = CD = a; AD = 2а. Знайти ∠A, ∠B, ∠BOC. За умовою AB = BC, тому ∆ABC — рівнобедрений, ∠BAC = ∠BCA. Крім того, ∠BCA = ∠CAD як внутрішні різносторонні кути з січною AC та паралельними прямими BC і AD. Тоді ∠BAC = ∠CAD = 1/2∠A. Так само ∠ADB = ∠BDC = 1/2∠D. Отже, ∠BAC = ∠BCA = ∠CAD = ∠ADB = ∠CDB = ∠CBD = 1/2∠А. Далі, сума кутів, прилеглих до бічної сторони трапеції, дорівнює 180°, тобто ∠A + ∠B = 180°. Зробимо допоміжну побудову: BM ⊥ AD і CN ⊥ ⊥ AD, тоді BCNM — прямокутник і MN = BC = а як протилежні сторони прямокутника. ∆ABM і ∆CDM — прямокутні і рівні (за гіпотенузою і катетом: AB = CD; BM = CN), AM = ND; але АМ + ND = AD – MN = AD – BC = 2а – а = а, тоді AM = 1/2а = 1/2АB. Це означає, що в ∆ABM ∠ABM = 30°, тобто ∠A = 60°. Отже, ∠B = 180° – ∠A = 180° – 60° = 120°. Таким чином, ∠A = 60°, ∠B = 120°, ∠BOC = 120°.