Назад
ГДЗ Геометрія 7 клас Бурда
Роздiл 5. Коло i круг
Реклама:
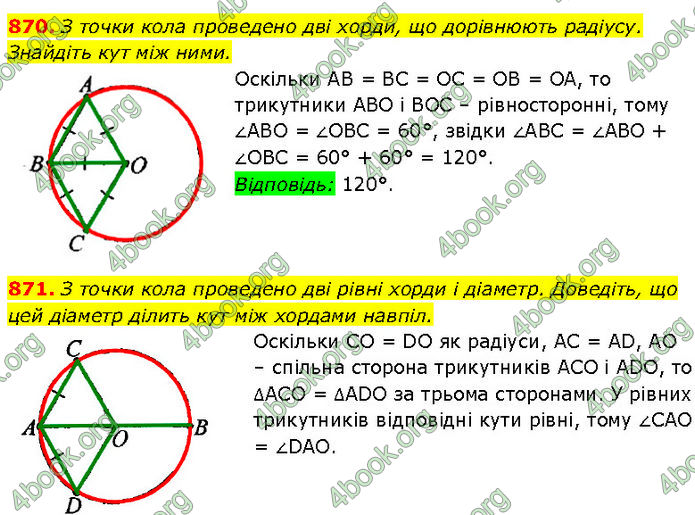
870. З точки кола проведено дві хорди, що дорівнюють радіусу. Знайдіть кут між ними.
Оскільки AB = BC = ОС = ОВ = ОА, то трикутники АВО і ВОС – рівносторонні, тому ∠АВО = ∠ОBC = 60°, звідки ∠ABC = ∠АВО + ∠ОВС = 60° + 60° = 120°.
Відповідь: 120°.
871. З точки кола проведено дві рівні хорди і діаметр. Доведіть, що цей діаметр ділить кут між хордами навпіл.
Оскільки CO = DO як радіуси, AC = AD, AO – спільна сторона трикутників ACO і ADO, то ∆ACO = ∆ADO за трьома сторонами.
У рівних трикутників відповідні кути рівні, тому ∠САО = ∠DAO.
Оскільки AB = BC = ОС = ОВ = ОА, то трикутники АВО і ВОС – рівносторонні, тому ∠АВО = ∠ОBC = 60°, звідки ∠ABC = ∠АВО + ∠ОВС = 60° + 60° = 120°.
Відповідь: 120°.
871. З точки кола проведено дві рівні хорди і діаметр. Доведіть, що цей діаметр ділить кут між хордами навпіл.
Оскільки CO = DO як радіуси, AC = AD, AO – спільна сторона трикутників ACO і ADO, то ∆ACO = ∆ADO за трьома сторонами.
У рівних трикутників відповідні кути рівні, тому ∠САО = ∠DAO.






