ГДЗ Геометрія 7 клас Бурда

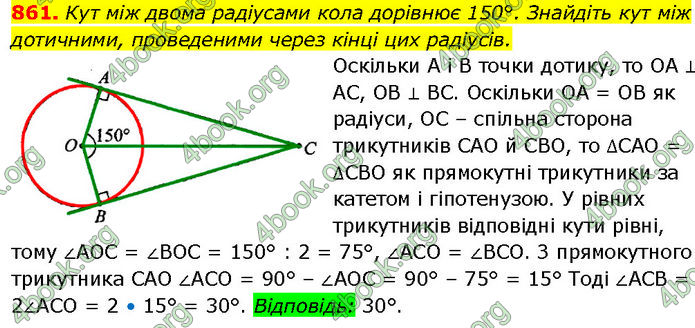
Кут між двома радіусами кола дорівнює 150°. Знайдіть кут між дотичними, проведеними через кінці цих радіусів.

Оскільки А і В точки дотику, то ОА ⊥ АС, ОВ ⊥ BC.
Оскільки ОА = ОВ як радіуси, ОС – спільна сторона трикутників CАO й СВО, то ∆CАO = ∆СВО як прямокутні трикутники за катетом і гіпотенузою.
У рівних трикутників відповідні кути рівні, тому ∠АОС = ∠ВОС = 150° : 2 = 75°, ∠АСО = ∠ВСО.
З прямокутного трикутника CАO ∠АСО = 90° – ∠АОС = 90° – 75° = 15° Тоді ∠АСВ = 2∠АСО = 2 • 15° = 30°.
Відповідь: 30°.