ГДЗ Геометрія 7 клас Бурда

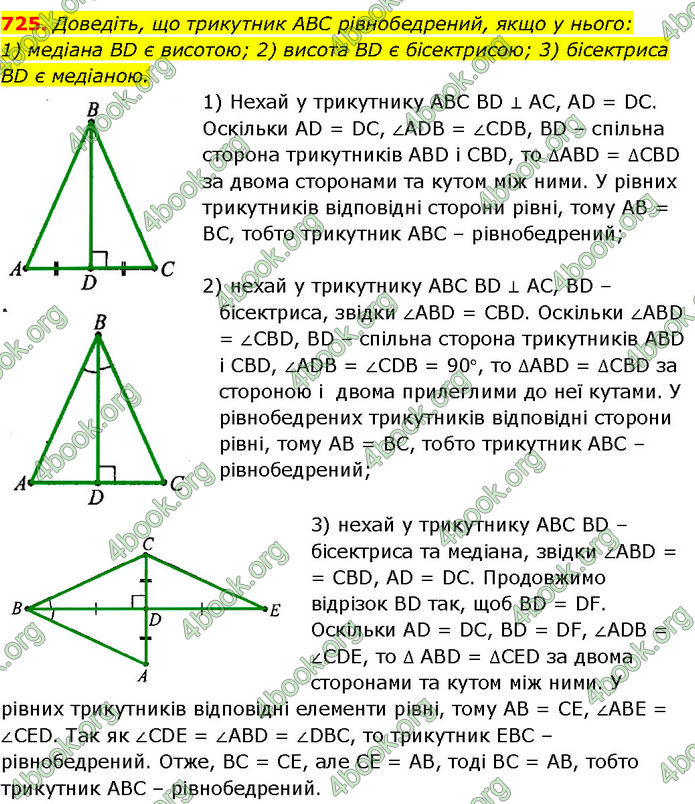
Доведіть, що трикутник ABC рівнобедрений, якщо у нього: 1) медіана BD є висотою; 2) висота BD є бісектрисою; 3) бісектриса BD є медіаною.

1) Нехай у трикутнику АВС BD ⊥ AC, AD = DC. Оскільки AD = DC, ∠ADB = ∠CDB, BD – спільна сторона трикутників ABD і CBD, то ∆ABD = ∆CBD за двома сторонами та кутом між ними. У рівних трикутників відповідні сторони рівні, тому АВ = ВС, тобто трикутник АВС – рівнобедрений;
2) нехай у трикутнику АВС BD ⊥ AC, BD – бісектриса, звідки ∠ABD = CBD. Оскільки ∠ABD = ∠CBD, BD – спільна сторона трикутників ABD і CBD, ∠ADB = ∠CDB = 90°, то ∆ABD = ∆CBD за стороною і двома прилеглими до неї кутами. У рівнобедрених трикутників відповідні сторони рівні, тому АВ = ВС, тобто трикутник АВС – рівнобедрений;
3) нехай у трикутнику АВС BD – бісектриса та медіана, звідки ∠ABD = CBD, AD = DC. Продовжимо відрізок BD так, щоб BD = DF. Оскільки AD = DC, BD = DF, ∠ADB = ∠CDE, то ∆ ABD = ∆CED за двома сторонами та кутом між ними. У рівних трикутників відповідні елементи рівні, тому АВ = СЕ, ∠АВЕ = ∠CED. Так як ∠CDE = ∠ABD = ∠DBC, то трикутник ЕВС – рівнобедрений. Отже, ВС = СЕ, але СЕ = АВ, тоді ВС = АВ, тобто трикутник АВС – рівнобедрений.