ГДЗ Геометрія 8 клас Мерзляк (2025)

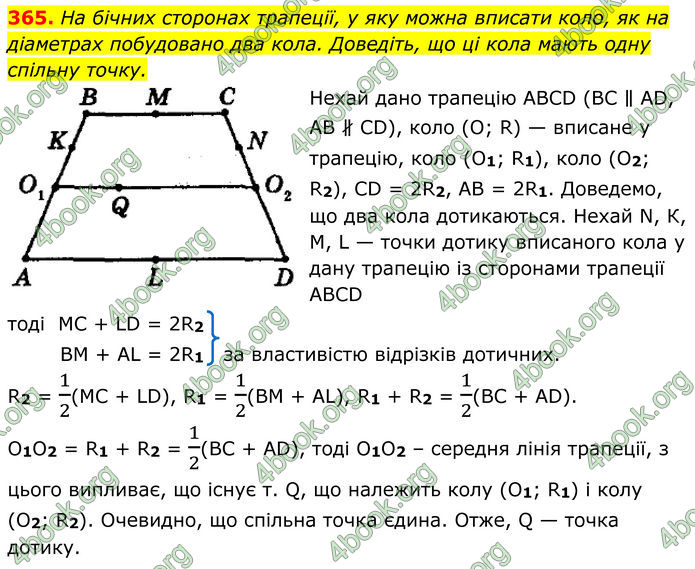
На бічних сторонах трапеції, у яку можна вписати коло, як на діаметрах побудовано два кола. Доведіть, що ці кола мають одну спільну точку.

Нехай дано трапецію АВСD (ВС ∥ АD, АВ ∦ СD), коло (О; R) — вписане у трапецію, коло (О1; R1), коло (O2; R2), СD = 2R2, АВ = 2R1. Доведемо, що два кола дотикаються.
Нехай N, К, М, L — точки дотику вписаного кола у дану трапецію із сторонами трапеції АВСD тоді МС + LD = 2R2 ВМ + АL = 2R1 за властивістю відрізків дотичних.
R2 = 1/2(MC + LD), R1 = 1/2(BM + AL), R1 + R2 = 1/2(ВС + AD). O1O2 = R1 + R2 = 1/2(ВС + AD), тоді О1О2 – середня лінія трапеції, з цього випливає, що існує т. Q, що належить колу (O1; R1) і колу (О2; R2).
Очевидно, що спільна точка єдина. Отже, Q — точка дотику.