ГДЗ Геометрія 8 клас Мерзляк (2025)

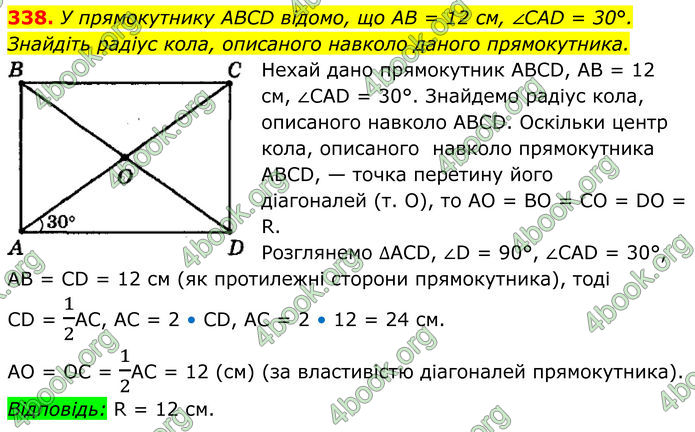
У прямокутнику ABCD відомо, що AB = 12 см, ∠CAD = 30°. Знайдіть радіус кола, описаного навколо даного прямокутника.

Нехай дано прямокутник ABCD, АВ = 12 см, ∠CAD = 30°.
Знайдемо радіус кола, описаного навколо ABCD.
Оскільки центр кола, описаного навколо прямокутника ABCD, — точка перетину його діагоналей (т. О), то АО = ВО = СО = DO = R.
Розглянемо ∆ACD, ∠D = 90°, ∠CAD = 30°, АВ = CD = 12 см (як протилежні сторони прямокутника), тоді CD = 1/2АС, АС = 2 • CD, АС = 2 • 12 = 24 см.
AO = OC = 1/2AC = 12 (см) (за властивістю діагоналей прямокутника).
Відповідь: R = 12 см.