ГДЗ Геометрія 8 клас Мерзляк (2025)

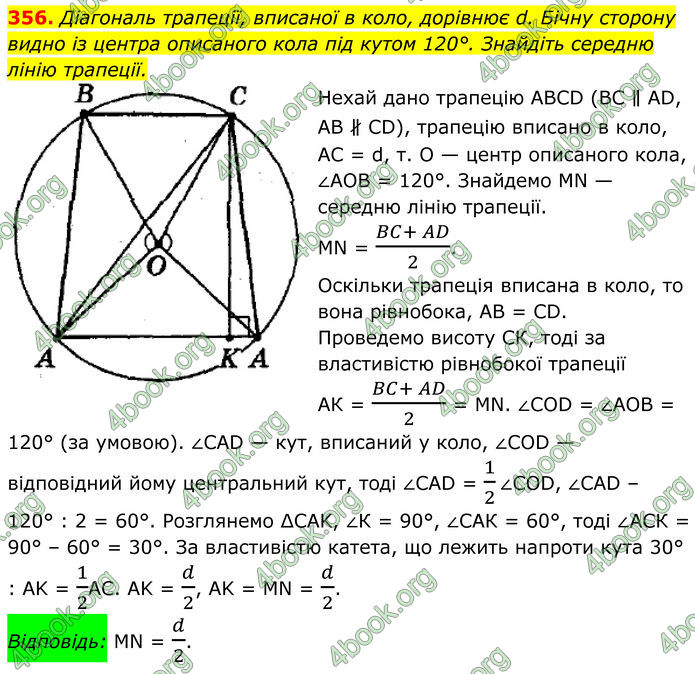
Діагональ трапеції, вписаної в коло, дорівнює d. Бічну сторону видно із центра описаного кола під кутом 120°. Знайдіть середню лінію трапеції.

Нехай дано трапецію ABCD (BC ∥ AD, AB ∦ CD), трапецію вписано в коло, AC = d, т. О — центр описаного кола, ∠АОВ = 120°.
Знайдемо MN — середню лінію трапеції. MN = (BC+ AD)/2.
Оскільки трапеція вписана в коло, то вона рівнобока, АВ = СD.
Проведемо висоту СК, тоді за властивістю рівнобокої трапеції АК = (BC+ AD)/2 = MN.
∠COD = ∠АОВ = 120° (за умовою). ∠CAD — кут, вписаний у коло, ∠COD — відповідний йому центральний кут, тоді ∠CAD = 1/2∠COD, ∠CAD – 120° : 2 = 60°.
Розглянемо ∆CAK, ∠К = 90°, ∠САК = 60°, тоді ∠АСК = 90° – 60° = 30°.
За властивістю катета, що лежить напроти кута 30° : AK = 1/2AC. AK = d/2, AK = MN = d/2.
Відповідь: MN = d/2.