ГДЗ Геометрія 8 клас Мерзляк (2025)

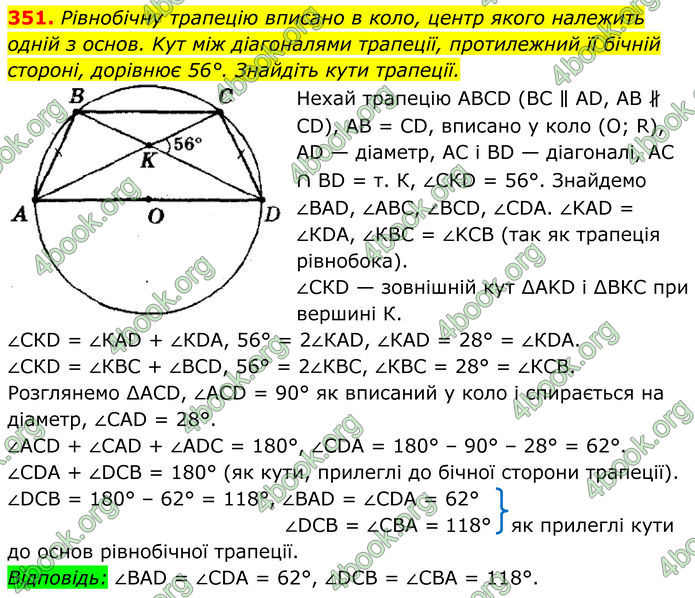
Рівнобічну трапецію вписано в коло, центр якого належить одній з основ. Kут між діагоналями трапеції, протилежний її бічній стороні, дорівнює 56°. Знайдіть кути трапеції.

Нехай трапецію АВСD (ВС ∥ АD, АВ ∦ СD), АВ = СD, вписано у коло (О; R), АD — діаметр, АС і ВD — діагоналі, АС ∩ ВD = т. К, ∠СКD = 56°.
Знайдемо ∠ВАD, ∠АВС, ∠ВСD, ∠CDA. ∠KАD = ∠КDА, ∠КВС = ∠KСВ (так як трапеція рівнобока).
∠СКD — зовнішній кут ∆АKD і ∆ВКС при вершині К.
∠СКD = ∠КАD + ∠КDА, 56° = 2∠КАD, ∠КАD = 28° = ∠КDА. ∠СКD = ∠КВС + ∠ВСD, 56° = 2∠КВС, ∠КВС = 28° = ∠КСВ.
Розглянемо ∆АСD, ∠АСD = 90° як вписаний у коло і спирається на діаметр, ∠САD = 28°. ∠АСD + ∠САD + ∠АDС = 180°, ∠СDА = 180° – 90° – 28° = 62°.
∠СDА + ∠DСВ = 180° (як кути, прилеглі до бічної сторони трапеції).
∠DCB = 180° – 62° = 118°, ∠BАD = ∠СDА = 62° ∠DCВ = ∠СВА = 118° як прилеглі кути до основ рівнобічної трапеції.
Відповідь: ∠ВАD = ∠СDА = 62°, ∠DСВ = ∠СВА = 118°.