ГДЗ Геометрія 8 клас Мерзляк (2025)

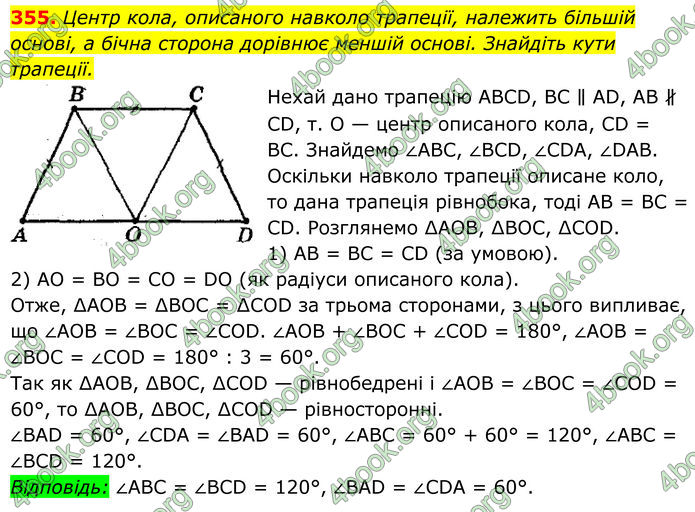
Центр кола, описаного навколо трапеції, належить більшій основі, а бічна сторона дорівнює меншій основі. Знайдіть кути трапеції.

Нехай дано трапецію ABCD, ВС ∥ AD, АВ ∦ CD, т. О — центр описаного кола, CD = ВС.
Знайдемо ∠ABC, ∠BCD, ∠CDA, ∠DAB.
Оскільки навколо трапеції описане коло, то дана трапеція рівнобока, тоді АВ = ВС = CD.
Розглянемо ∆АОВ, ∆ВОС, ∆COD. 1) АВ = ВС = CD (за умовою).
2) AO = BO = CO = DO (як радіуси описаного кола).
Отже, ∆АОВ = ∆ВОС = ∆COD за трьома сторонами, з цього випливає, що ∠АОВ = ∠ВОС = ∠COD.
∠АОВ + ∠ВОС + ∠COD = 180°, ∠АОВ = ∠ВОС = ∠COD = 180° : 3 = 60°.
Так як ∆АОВ, ∆ВОС, ∆COD — рівнобедрені і ∠АОВ = ∠ВОС = ∠COD = 60°, то ∆АОВ, ∆ВОС, ∆COD — рівносторонні.
∠BAD = 60°, ∠CDA = ∠BAD = 60°, ∠ABC = 60° + 60° = 120°, ∠ABC = ∠BCD = 120°.
Відповідь: ∠ABC = ∠BCD = 120°, ∠BAD = ∠CDA = 60°.